はじめに #
本記事は以下の記事の続きである。等式制約を2つ持つ最適化問題をラグランジュの未定乗数法で解き、その幾何学的な意味を示す。
例題(承前) #
例題2 等式制約が2つある場合 #
2次元ベクトル\(\boldsymbol{x}=(x_1, x_2)\)に対して、次式の等式制約を2つ持つ最小化問題を考える。
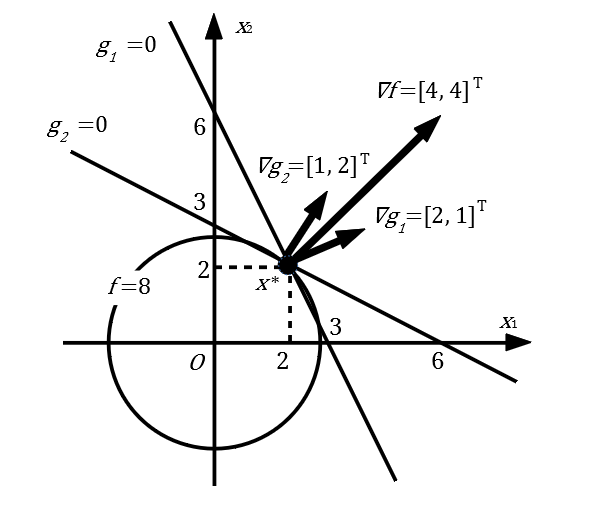
$$ \begin{array}{ll} \mathrm{min} \ & f(\boldsymbol{x}) = x_1^2 + x_2^2 \\ \mathrm{s.t.}\ & g_1(\boldsymbol{x}) = x_1 + 2 x_2 - 6 = 0 \\ & g_2(\boldsymbol{x}) = 2 x_1 + x_2 - 6 = 0 \end{array} $$上記の\(f\)は凸関数かつ、\(g_i\)は全て1次式であるから、ラグランジュの未定乗数法で得られる解は最適解になる。なお、最適解は\((x_1, x_2)=(2, 2)\)となり、最小値\(f=8\)を得る(下図参照)。
上記の問題のラグランジュ関数は次式で与えられる。
$$ L(\boldsymbol{x}, \boldsymbol{\lambda}) = x_1^2 + x_2^2 - \lambda_1 (x_1 + 2 x_2 - 6) - \lambda_2 (2 x_1 + x_2 - 6) $$最適解は、このラグランジュ関数の勾配ベクトルの各成分が0となる\(\boldsymbol{x}\)である。よって、次の連立方程式が得られる。
$$ \nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\lambda}) = \left[ \begin{array}{l} \frac{\partial L}{\partial x_1} \\ \frac{\partial L}{\partial x_2} \end{array} \right] = \left[ \begin{array}{l} 2 x_1 - \lambda_1 - 2 \lambda_2 \\ 2 x_2 - 2 \lambda_1 - \lambda_2 \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] $$$$ \nabla_{\boldsymbol{\lambda}} L(\boldsymbol{x}, \boldsymbol{\lambda}) = \left[ \begin{array}{l} \frac{\partial L}{\partial \lambda_1} \\ \frac{\partial L}{\partial \lambda_2} \end{array} \right] = \left[ \begin{array}{l} - (x_1 + 2 x_2 - 6) \\ - (2 x_1 + x_2 - 6) \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] $$連立方程式を解くと、以下の解が得られる。
$$ (x_1, x_2, \lambda_1, \lambda_2) = \left(2, 2, \frac{4}{3}, \frac{4}{3} \right) $$したがって、最適解は\(\boldsymbol{x}^*=(2, 2)\)となる。このとき、目的関数は\(f=8\)となる。
また、最適解における評価関数と等式制約の各勾配ベクトルは以下のようになる。
$$ \nabla f(\boldsymbol{x}^*) = \left[ \begin{array}{l} 4 \\ 4 \end{array} \right] $$$$ \nabla g_1(\boldsymbol{x}^*) = \left[ \begin{array}{l} 2 \\ 1 \end{array} \right]$$$$ \nabla g_2(\boldsymbol{x}^*) = \left[ \begin{array}{l} 1 \\ 2 \end{array} \right] $$ここで、\((\lambda_1, \lambda_2)=(4/3, 4/3)\)であるから、次式が成り立つ。
$$ \nabla f(\boldsymbol{x}^*) = \lambda_1 \nabla g_1(\boldsymbol{x}^*) + \lambda_2 \nabla g_2(\boldsymbol{x}^*) $$$$ \left[ \begin{array}{l} 4 \\ 4 \end{array} \right] = \frac{4}{3}\left[ \begin{array}{l} 2 \\ 1 \end{array} \right] + \frac{4}{3} \left[ \begin{array}{l} 1 \\ 2 \end{array} \right] $$すなわち、最適解において、評価関数の勾配ベクトルと、等式制約の勾配ベクトルの線形和は等しい。
