はじめに #
ラグランジュの未定乗数法は制約条件を持つ最適化問題を解くための手法である。この手法は非線形問題に対して適用でき、内点法や有効制約法などにおいても利用されている。
ラグランジュの未定乗数法では、制約条件に定数(ラグランジュ乗数)を掛けて目的関数と線形結合したラグランジュ関数と呼ばれる関数を定義する。この関数の極値を求めると、局所最適解が得られる(問題が特定の条件を満たせば最適解が得られる)。
また、ラグランジュの未定乗数法は、等式制約を持つ場合、不等式制約を持つ場合、またはそれら両方を持つ場合のどちらでも適用できる。本記事では、等式制約のみ持つ場合を対象とする。
(※ただし、不等式制約はスラック変数を導入して等式制約に置き換えることができる。例えば、不等式制約\(g(x) \le 0\)は、スラック変数\(s \ge 0\)を用いて等式制約\(g(x)+s=0\)に置き換えられる。そのため、単に最適化問題を解くためであれば、等式制約のみ扱う手法のみ知っていれば実用上は問題ない)
対象とする問題 #
以下の等式制約付き非線形最小化問題を考える。
$$ \begin{array}{ll} & \mathrm{min} \ f(\boldsymbol{x}) \\ & \mathrm{s.t.}\ g_i(\boldsymbol{x})=0 \ (i=1, ..., m) \tag{1} \end{array} $$ここで、\(\boldsymbol{x} \in \mathbb{R}^n\), \(n \ge m\)とする。また、\(f, g\)は微分可能とする。
これは、等式制約\(g_i(\boldsymbol{x})=0\)をすべて満たし、関数\(f(\boldsymbol{x})\)を最小化する変数\(\boldsymbol{x}\)を求める問題となる。
ラグランジュの未定乗数法 #
上記の問題に対して、次式の関数を定義する。
$$ \begin{array}{ll} L(\boldsymbol{x}, \boldsymbol{\lambda}) & = f(\boldsymbol{x}) - \boldsymbol{\lambda}^{\top} \boldsymbol{g}(\boldsymbol{x}) \\ & = f(\boldsymbol{x}) - \sum_{i=1}^{m} \lambda_i g_i(\boldsymbol{x}) \end{array} \tag{2} $$これをラグランジュ関数と呼ぶ。また、\(\lambda_i (i=1, ..., m)\)をラグランジュ乗数、\(\boldsymbol{\lambda}\)をラグランジュ乗数ベクトルと呼ぶ。
等式付き制約問題の局所解を \( \boldsymbol{x}^* \) とすると、 \( \boldsymbol{x}^* \) は次の等式を満たす。
$$ \nabla_{\boldsymbol{x}} L(\boldsymbol{x}^*, \boldsymbol{\lambda}^*) = \nabla f(\boldsymbol{x}^*) - \sum_{i=1}^{m} \lambda_i^* \nabla g_i(\boldsymbol{x^*}) = \boldsymbol{0} \tag{3} $$$$ \nabla_{\boldsymbol{\lambda}} L(\boldsymbol{x}^*, \boldsymbol{\lambda}^*) = \boldsymbol{g} (\boldsymbol{x^*}) = \boldsymbol{0} \tag{4} $$すなわち、ラグランジュ関数の勾配ベクトルの各成分が0となる値が最適解となる。
式(3)を変形すると次式を得る。
$$ \nabla f(\boldsymbol{x}^*) = \sum_{i=1}^{m} \lambda_i^* \nabla g_i(\boldsymbol{x^*}) \tag{5} $$これは、等式制約\(g_i\)の勾配ベクトルに、あるラグランジュ乗数\(\lambda_i^*\)を掛けた合成ベクトルと、目的関数\(f\)の勾配ベクトルが平行であることを意味する。
なお、\(f\)が凸関数かつ、\(g_i\)が全て1次式ならば、\(\boldsymbol{x}^*\)は最適解になる。これはKKT条件(Karush-Kuhn-Tucker条件)から得られるが、本記事ではこれ以上触れない。
また、式(4)は、局所解が元の最適化問題の等式制約を満たすことを示す。
例題 #
以下の2つの例題に対して、ラグランジュの未定乗数法を適用し、幾何学的な意味を示す。
- 等式制約が1つだけの場合
- 等式制約が2つある場合(後編の記事に分割)
例題1 等式制約が1つだけの場合 #
2次元ベクトル\(\boldsymbol{x}=(x_1, x_2)\)に対して、次式の等式制約を1つだけ持つ最小化問題を考える。
$$ \begin{array}{ll} & \mathrm{min} \ f(\boldsymbol{x}) = x_1^2 + x_2^2 \\ & \mathrm{s.t.}\ g(\boldsymbol{x}) = x_1 + x_2 - 2 = 0 \end{array} $$上記の\(f\)は凸関数かつ、\(g_i\)は全て1次式であるから、ラグランジュの未定乗数法で得られる解は最適解になる。なお、最適解は\((x_1, x_2)=(1, 1)\)となり、最小値\(f=2\)を得る(下図参照)。
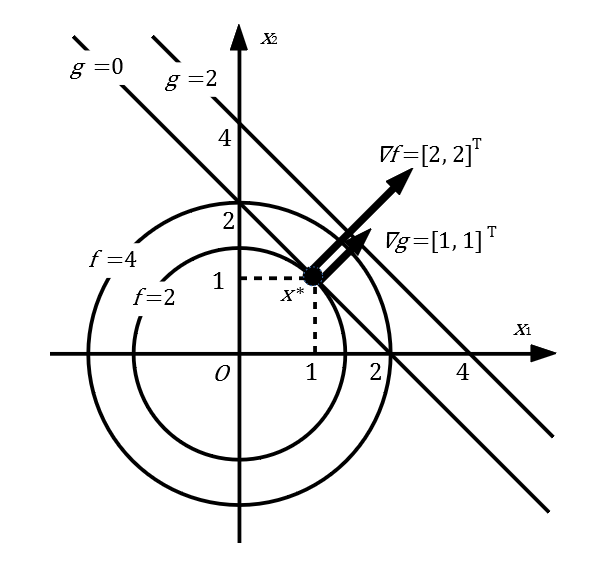
上記の問題のラグランジュ関数は次式で与えられる。
$$ L(\boldsymbol{x}, \boldsymbol{\lambda}) = x_1^2 + x_2^2 - \lambda (x_1 + x_2 -2) $$最適解は、このラグランジュ関数の勾配ベクトルの各成分が0となる\(\boldsymbol{x}\)である。よって、次の連立方程式が得られる。
$$ \nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\lambda}) = \left[ \begin{array}{l} \frac{\partial L}{\partial x_1} \\ \frac{\partial L}{\partial x_2} \end{array} \right] = \left[ \begin{array}{l} 2 x_1 - \lambda \\ 2 x_2 - \lambda \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] $$$$ \nabla_{\boldsymbol{\lambda}} L(\boldsymbol{x}, \boldsymbol{\lambda}) = - (x_1 + x_2 - 2) = 0 $$連立方程式を解くと、以下の解が得られる。
$$ (x_1, x_2, \lambda) = (1, 1, 2) $$したがって、最適解は\(\boldsymbol{x}^*=(1, 1)\)となる。このとき、目的関数は\(f=2\)となる。
\(\nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\lambda})\)は、最適解において評価関数\(f\)の勾配ベクトルと等式制約\(g\)の勾配ベクトルが平行であることを意味する。各勾配ベクトルは、
$$ \nabla f(\boldsymbol{x}) = \left[ \begin{array}{l} 2 x_1 \\ 2 x_2 \end{array} \right] $$$$ \nabla g(\boldsymbol{x}) = \left[ \begin{array}{l} 1 \\ 1 \end{array} \right] $$
となる。最適解における\(f\)の勾配ベクトルは、
$$ \nabla f(\boldsymbol{x}^*) = \left[ \begin{array}{l} 2 \\ 2 \end{array} \right] $$であるから、\(\nabla g(\boldsymbol{x})\)に平行である。言い換えると、最適解において、\(f\)の等高線と\(g\)の接線は一致する。
等式制約が2つある場合については後編の記事を参照。
