はじめに #
DBSCANはk-means法と並んでよく用いられるクラスタリング手法です。DBSCANはDensity-Based Spatial Clustering of Applications with Noiseの略で、「ノイズ付きのデータに適用可能な密度ベースの空間的クラスタリング」という意味です。
DBSCANには以下の長所があります。
- k-means法と比較して実行が遅いが、ある程度大規模なデータにも適用できる。
- ユーザがクラスタリング数を決める必要がない。
この手法は、あるクラスタに属するデータは密集しており、クラスタ同士の空間は比較的空虚(スパース)であることを仮定しています。
また、この記事ではPythonとScikit-learnによるサンプルコードも示します。実行環境は以下の通りです。
- Python: 3.9.7
- NumPy: 1.20.3
- sklearn: 0.24.2
- matplotlib: 3.4.3
アルゴリズム #
DBSCAN法のアルゴリズムは次の通りです。
- 適当にデータを1点選択する。
- そのデータ点から距離\(\epsilon\)以内にあるデータ点数を数える。
- 2.のデータ点数がしきい値\(N_{min}\)未満であれば、そのデータを「ノイズ」に分類して8.に映る。
- 2.のデータ点数が\(N_{min}\)以上であれば、1.の点を「コア点」と呼び、新しいクラスタのラベルを割り当てる。
- コア点から距離\(\epsilon\)以内にある未分類のデータに対して、4.と同じラベルを割り当て、同様に距離\(\epsilon\)以内にあるデータ点数を数える。
- 5.のデータ点数が\(N_{min}\)未満であれば「到達可能点」(または境界点)と呼ぶ。
- 5.のデータ点数が\(N_{min}\)以上あればコア点として、5.に戻ってさらに近傍のデータ点を調べる。
- まだ調べていない点があれば、1.に戻る。全ての点を調べ終わると終了する。
データ点は、コア点、到達可能点、ノイズのいずれかに分類されます。また、クラスタは、その周囲\(\epsilon\)以内にコア点が存在しなくなるまで成長します。
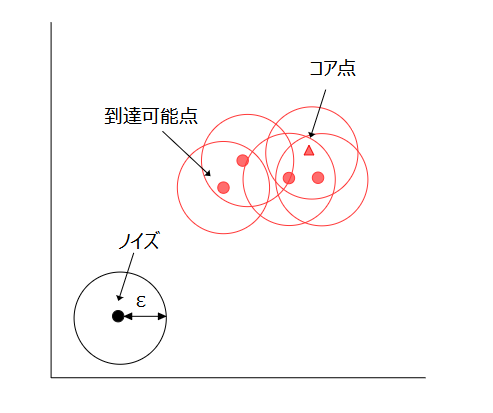
DBSCANを同じデータに対して実行すると、コア点とノイズは常に同じデータになります。一方、到達可能点がどのクラスタに属するか異なる場合があります。これは、到達可能点は複数のクラスタ同士の境界にあることが多く、形成されるクラスタの順番に依存するためです。
DBSCANでは、新たにデータが与えられた場合はクラスタの予測ができません(学習を最初からやり直す必要があります)。
scikit-learnのDBSCAN法 #
DBSCANクラス #
scikit-learnではsklearn.cluster.DBSCANというクラスにDBSCAN法が実装されています。
class klearn.cluster.DBSCAN(eps=0.5, min_samples=5,
metric='euclidean', metric_params=None, algorithm='auto',
leaf_size=30, p=None, n_jobs=None)
主なパラメータの意味は以下の通りです。
eps(float): コア点から探索する距離(デフォルトは0.5)。min_samples(int): コア点をクラスタとして判定する最小データ点数(デフォルトは5)。n_jobs(int): 並列計算数を指定します。-1にすると全てのCPUコアを使用します。
また、主なメソッドは以下の通りです。
fit(X): 特徴量X(サンプル数×特徴量数の2次元配列)をクラスタリングする。fit_predict(X): 特徴量Xをクラスタリングし、結果を返す。
使用例 #
DBSCANクラスの使用例を示します。X_trainは行がサンプル、列が特徴量の2次元配列です(PandasのDataFrameなどでも可)。DBSCANクラスのオブジェクトをdbscanという名前で作成し、fit_predictでクラスタリングを行います。ここで、分析するデータに合わせてパラメータeps, min_samplesを設定しています。
import numpy as np
from sklearn.cluster import DBSCAN
# 学習データ
X_train = np.array([[0, 0],
[0, 1],
[0, 2],
[2, 0],
[3, 0],
[4, 5],
[5, 4],
[2, 4]])
dbscan = DBSCAN(eps=1.5, min_samples=2)
cluster_pred = dbscan.fit_predict(X_train)
print(cluster_pred)
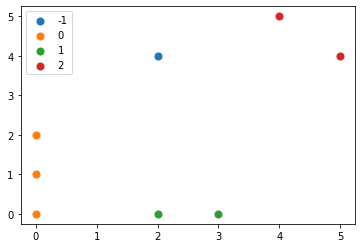
実行結果:クラスタリングの結果は以下になりました。1~3番目のデータはクラスタ0, 4, 5番目のデータはクラスタ1, …, に属することを示しています。また、ノイズに分類されたデータは-1となります。
[ 0 0 0 1 1 2 2 -1]
最後に、クラスタリングの結果をMatplotlibを使って図示します。
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
for i in range(-1, max(cluster_pred)+1):
x = X_train[cluster_pred==i]
ax.scatter(x[:,0], x[:,1], s=50, label=i)
ax.legend()
plt.show()
実行結果:クラスタによって色が異なるようにしています。近くにあるデータ同士が同じクラスタに含まれることが分かります。