はじめに #
分類木 (classification tree) は、分析したデータが属するカテゴリー(クラス)を予測する分類アルゴリズムの1つです。分類木では、Yes/Noによる分岐を何度か繰り返して、分類の予測を返します。
簡単な例として、クジラ、サメ、馬、犬を分類する問題を考えます。分類木では、なるべく少ない質問で答えを返せるようにします。まず、「海に住んでいるか?」という質問を用意すると、クジラとサメが該当します。さらに、「哺乳類か?」という質問を考えるとクジラとサメを分類できます。残った馬と犬は、「たてがみがあるか?」という質問で分類できます。
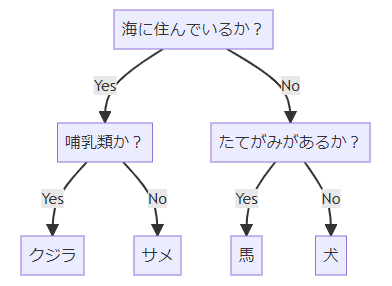
なお、このフローチャートも分類木と呼びます。さらに、分類木の質問や分類結果の四角のことをノード (node) と呼びます。ノードの内、末端の分岐しないものを葉 (leaf) と呼びます
また、分類木に似たアルゴリズムとして、カテゴリを予測するのではなく、予測値を返す回帰木 (regression tree) があります。分類木と回帰木を合わせて、決定木 (decision tree) と呼びます。
分類木のアルゴリズム #
分類木のアルゴリズムをより詳しく説明します。
3つのアヤメの品種を分類する問題を考えます。品種の名前はそれぞれsetosa, versicolor, virginicaです。また、使用する特徴量は花弁の幅 (petal width) とガクの長さ (sepal length) の2つとします。データを以下のグラフに示します。
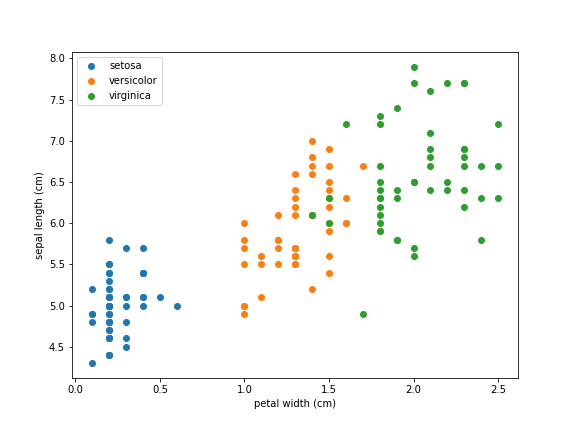
このデータに対して構築した分類木の例を以下に示します。
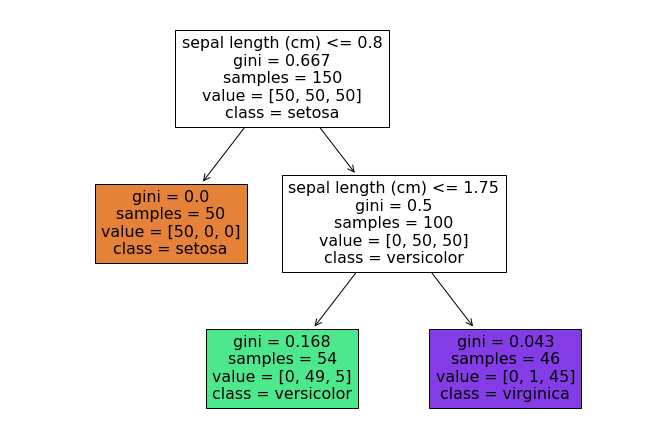
この分類木を見ると、最初にsepal lengthが0.8以下であればsetosaに分類されることが分かります。残りのデータに対して、sepal lengthが1.75以下であればversicolor, 1.75より大きければvirginicaに分類されます。petal widthは分類に用いられないことが分かります。
分類木がどの特徴量やしきい値で分類するかは、ある指標に基づいて決まります。指標について次節で解説します。
分類の指標 #
分類木のアルゴリズムに使用される主な指標として、ジニ不純度 (Gini impurity) とエントロピー (entropy) があります。先ほどの例では、ジニ不純度が使用されています。大半のケースでは、ジニ不純度とエントロピーのどちらを使用しても同じような分類結果になります。両者が異なるケースでは、ジニ不純度はデータ数が最も多いクラスをブランチ(枝)にまとめる傾向がある一方で、エントロピーは若干均衡がとれた分類木になりやすいです。なお、計算速度はジニ不純度の方がやや高速です。
ジニ不純度とエントロピーのどちらも、値が大きいほど様々なクラスのデータが均等に含まれていることを意味します。そのため、分類木では、これらの指標が小さくなるような特徴量やしきい値を決定します。以下では、ジニ不純度とエントロピーの計算式を示します。
ジニ不純度 #
ジニ不純度は0から1の間の値をとり、値が大きいほど不純度が高いです。\(i\)番目のノードのジニ不純度\(G_i\)は次式で計算されます。
$$ G_i = 1 - \sum_{k=1}^{c} p_{i,k}^2 $$ここで、\(c\)はクラスの数、\(p_{i,k}\)は\(i\)番目のノードに\(k\)番目のクラスのデータが属する割合を示します。
ジニ不純度の値を計算してみます。クラスが3つあり、それぞれのデータが2個ずつある場合のジニ不純度は次式で計算されます。
$$ G_i = 1 - \sum_{k=1}^{3} \left( \frac{2}{6} \right)^2 \approx 0.667$$次に、クラス3つに対して、1つのクラスに属するデータ2つのみがある場合、ジニ不純度は次式で計算されます。
$$ G_i = 1 - \left( \left( \frac{2}{2} \right)^2 + 0 + 0 \right) = 0$$すなわち、分類木のあるノードに属するデータが全て同じ(純粋)である場合、ジニ不純度は0になります。
エントロピー #
エントロピーは熱力学を始めとして、様々な分野で用いられる言葉です。情報理論の分野では、メッセージに含まれる情報の多さを表します。分類木の場合は、値が大きいほど様々なクラスのデータが含まれることを意味します。\(i\)番目のノードのエントロピー\(H_i\)は次式で計算されます。
$$ H_i = - \sum_{k=1}^{c} p_{i,k} \log(p_{i,k}) $$ここで、\(c\)はクラスの数、\(p_{i,k}\)は\(i\)番目のノードに\(k\)番目のクラスのデータが属する割合を示します。エントロピーは0以上の値を取ります。
ジニ不純度と同様にエントロピーの値を計算してみます。クラスが3つあり、それぞれのデータが2個ずつある場合のエントロピーは次式で計算されます。
$$ H_i = - \sum_{k=1}^{3} \left( \frac{2}{6} \log \left( \frac{2}{6} \right) \right) \approx 0.4515$$次に、クラス3つに対して、1つのクラスに属するデータ2つのみがある場合、エントロピーは次式で計算されます。
$$ H_i = - \frac{2}{2} \log \left( \frac{2}{2} \right) = 0$$ジニ不純度と同じく、分類木のあるノードに属するデータが全て同じ(純粋)である場合、エントロピーは0になります。
過学習の抑制 #
ノードに含まれるデータが純粋(同じクラスのみ)になるまで分類木を分岐をさせると、過学習 (overfitting) が起こり、モデルが複雑になり過ぎてしまいます。過学習を防ぐ手段として、事前枝刈り (pre-pruning) と事後枝刈り (post-pruning) の2つがあります。事前枝刈りは、分類木の構築過程で、木の深さ、葉の最大値を制限したり、ノードに含まれるデータ数の最小値を決めておくものです。一方、事後枝刈りは、一度分類木を構築してから、情報が少ないノードを削除します。
長所と短所 #
分類木の長所は、学習したモデルを可視化しやすく、理解や解釈がしやすい点です。また、特徴量の分割はスケールに依存しないため、特徴量を正規化・標準化するなどのスケール変換は不要です。また、特徴量に離散変数や連続変数が混在している場合にも適用できます。
一方、分類木にはいくつかの短所もあります。1つ目は、決定境界が特徴量の座標に直交することです。そのため、決定境界を斜めに引いた方がうまく分類できるケースでは、性能が悪くなります。この問題は、特徴量を主成分分析 (PCA, principal component analysis) で変換することにより少し低減できます。2つ目は、事前枝刈りなどを行っても学習データに過剰に適合して、汎化性能が低くなりやすいことです。この課題に対処するため、分類木を発展させたランダムフォレストという手法が用いられます。この手法は、1つの分類木で予測するのではなく、複数の分類木を組み合わせるもの(アンサンブル法)です。
scikit-learnの分類木 #
DecisionTreeClassifierクラス #
scikit-learnではsklearn.tree.DecisionTreeClassifierというクラスに決定木が実装されています。
sklearn.tree.DecisionTreeClassifier(*, criterion='gini',
splitter='best', max_depth=None, min_samples_split=2,
min_samples_leaf=1, min_weight_fraction_leaf=0.0,
max_features=None, random_state=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0)
主なパラメータの意味は以下の通りです。
criterion(str): 分割の指標。"gini"(ジニ不純度)、"entropy"(エントロピー)、"log_loss"から選択(デフォルトは"gini")。splitter(str): ノードごとの分割方法。"best"(指標が最も小さくなる特徴量で分割)、"random"(分割する特徴量をランダムに選ぶが、指標を小さくできる特徴量ほど選びやすくなるように重みを付けて選ぶ)から選択(デフォルトは"best")。
python - What does ‘splitter’ attribute in sklearn’s DecisionTreeClassifier do - Stack Overflowmax_depth(int/None): 分類木の最大深さ。Noneの場合は全ての葉のデータ数がmin_samples_split以下になるまで木を成長させる。min_samples_split(int/float): ノードを分割するときに必要な最小データの量。int型の場合、データ数。float型の場合、全体データ数n_samplesに対する割合(デフォルトは2)。 % -min_weight_fraction_leaf(float): 各葉に必要なデータの割合の最小値(デフォルトは0)。max_features(int/float/str): 分割に用いる特徴量の最大数。int型の場合、特徴量の数。float型の場合、全体の特徴量の数n_featuresに対する割合。"sqrt"や"log2"も指定可能(デフォルトは2)。random_state(int/None): 学習時の乱数シード。常に同じ結果を得たい場合は適当な整数を指定する。Noneの場合、結果は変わり得る(デフォルトはNone)。max_leaf_nodes(int/None): 最大の葉の数。Noneの場合、葉の数に制限を設けない(デフォルトはNone)。
また、主なメソッドは以下の通りです。
fit(X, y): 特徴量X, クラスyを教師データとして学習する。predict(X): 特徴量Xに対するクラスの予測結果を返す。predict_proba(X): 特徴量Xに対する各クラスの予測確率を返す。get_params([deep]): 分類木のパラメータを返す。get_depth(): 分類木の深さを返す。get_n_leaves(): 葉の数を返す。
使用例 #
DecisionTreeClassifierクラスの使用例を示します。実行環境は以下の通りです。
- Python: 3.9.7
- NumPy: 1.20.3
- sklearn: 0.24.2
X_trainは行がサンプル、列が特徴量の2次元配列です(PandasのDataFrameなどでも可)。y_trainは分類クラスの1次元配列です。次に、DecisionTreeClassifierクラスのオブジェクトをclfという名前で作成します(clfはclassifierから名付けています)。オプションで評価指標をエントロピーに設定しています。
import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
# 学習データ
X_train = np.array([[0, 1],
[1, 3],
[3, 2]])
y_train = np.array([0, 0, 1])
clf = DecisionTreeClassifier(criterion="entropy")
fitメソッドで学習し、predictメソッドで予測します。予測結果は1次元配列となります。
# 学習
clf.fit(X_train, y_train)
X_test = np.array([[0, 1],
[2.8, 2]])
# 予測
y_pred = clf.predict(X_test)
print(y_pred)
実行結果:
[0 1]
predict_probaメソッドで予測確率を返します(葉の同じクラスに属するデータの割合が確率になります)。
y_prob = clf.predict_proba(X_test)
print(y_prob)
実行結果:
[[1. 0.]
[0. 1.]]
