はじめに #
PyomoはPythonで書かれた最適化モデリングツールである。Pyomoの概要と基本的な使い方は以下の記事を参照。
GDPは最適化問題の表現の1つであり、Generalized Disjunctive Programming の頭文字をとったものである。直訳すると一般化離接計画問題となる。離接とは論理和 (OR) のことである。 GDPでは最適化問題における論理的な制約を表現できる。例えば、2つの等式制約があるが、どちらか片方のみ満たせば良い、という表現ができる。
本記事では、Pyomoを使ったGDP問題の定義、およびGDPソルバの実行方法についてまとめた。GDPを解くときにはMINLPなどに変換するが、詳細については触れない。
ソフトウェアのバージョンは以下の通り。
- Python 3.7.4
- Pyomo 5.6.9
- glpk 4.65
環境の設定 #
Pyomoに拡張機能としてGDPのモデリング機能が実装されているので、Pyomoと適当なソルバを導入する。ここでは、pyomoと線形ソルバGLPKをインストールする。
conda環境の場合は次の通り。
conda install -c conda-forge pyomo
conda install -c conda-forge glpk
pip環境の場合は次の通り。
pip install pyomo
pip install glpk
GDPの基本形 #
GDPの基本的な式は以下のように表記される(出展:Disjunctive Programming - GAMS)。

主な変数の意味は以下の通り。
- x: 変数
- f(x): 目的関数
- g(x): 不等式制約
- Y: ブーリアン
- L: xの下限
- U: xの上限
- Ω(Y): Yの論理制約
- r(x): 対応するYがTrueのときのみ有効な不等式制約
- n: 変数の数
- K: 論理和条件の数
また、記号Vは論理和を示す。
GDPは、化学プラントなどの最適な装置の組み合わせを求めるのに用いられる。プラントの生成物などが変数、利益などが目的関数になる。また、装置によって生成物の上限やコストなどは異なるが、このような条件が制約条件になる。
GDPの例 #
GDPの例を示す。2変数\(x_1, x_2\)に対して、目的関数\(x_1+x_2\)を最大化する問題を考える。実行可能領域は下図の斜線部とすると、\((x_1, x_2)=(10, 7)\)で大域的最適解\( 17\)をとる。
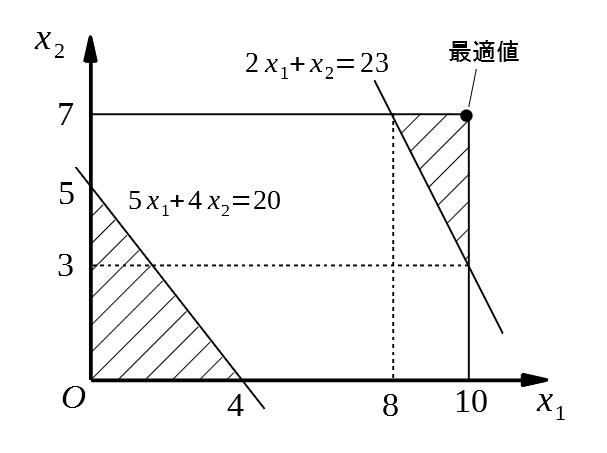
この問題をGDPで表すと次式のようになる。
$$ \begin{array}{ll} \text{maximize} & x_1 + x_2 \\\ \text{subject to} & \begin{bmatrix} Y_{1} \\\ 5x_1 + 4x_2 \le 20 \end{bmatrix} \vee \begin{bmatrix} Y_{2} \\\ 2x_1 + x_2 \ge 23 \end{bmatrix} \\\ & Y_1 \rightarrow \neg Y_2 \\\ & Y_2 \rightarrow \neg Y_1 \\\ & 0 \le x_1 \le 10, 0 \le x_2 \le 7, \\\ & Y_{1}, Y_{2} \in \{ \text{True, False} \} \end{array} $$ここで、¬は否定 (NOT) の意味である。上記の式では、Y1とY2の片方のみTrueになる。
なお、GDPの disjuntive は論理和 (OR) を意味するが、Pyomoの公式リファレンスや関連する論文を読むと、排他的論理和 (XOR) の意味でも用いられることが多いように思う。
PyomoでGDPを解く #
上記の例をpyomoで実装すると、以下のようになる。
import pyomo.environ as pe
import pyomo.gdp as pg
model = pe.ConcreteModel()
model.x1 = pe.Var(domain=pe.Reals, bounds=(0, 10))
model.x2 = pe.Var(domain=pe.Reals, bounds=(0, 7))
model.Y1 = pg.Disjunct()
model.Y1.c = pe.Constraint(expr = 5*model.x1+4*model.x2 <= 20)
model.Y2 = pg.Disjunct()
model.Y2.c = pe.Constraint(expr = 2*model.x1+model.x2 >= 23)
model.c = pg.Disjunction(expr=[model.Y1, model.Y2])
model.OBJ = pe.Objective(expr=model.x1+model.x2, sense=pe.maximize)
pe.SolverFactory('gdpopt').solve(model, mip_solver='glpk')
print(f"評価関数:{model.OBJ()}")
print(f"x1: {model.x1()}")
print(f"x2: {model.x2()}")
実行結果は以下のようになり、最適解を得られたことが分かる。
評価関数:17.0
x1: 10.0
x2: 7.0
ソースコードの解説 #
GDPに関する部分のみ、ソースコードを簡単に解説する。
model.Y1 = pg.Disjunct()
model.Y1.c = pe.Constraint(expr = 5*model.x1+4*model.x2 <= 20)
Disjunctクラスは、ブーリアンに相当する。上記のコードでは、model.Y1がTrueの場合のみ、model.Y1.cで定義された制約条件が有効になる。
model.c = pg.Disjunction(expr=[model.Y1, model.Y2])
Disjunctionクラスは、論理和の制約を示す。引数exprに渡した2つのDisjunctオブジェクトの内、どちらか片方のみTrueになることを示す。
※公式リファレンスでは"logical OR"という表現だが、実際は排他的論理和 (XOR) のように振る舞う。
pe.SolverFactory('gdpopt').solve(model, mip_solver='glpk')
ソルバにはGDPoptを指定する。ただし、GDPoptはGDPを変換するがMIPソルバを含んでいないので、GLPKを指定する。
参考 #
PyomoにおけるGDPのクラスについて
Generalized Disjunctive Programming — Pyomo 5.7.2 documentation
GDPoptソルバについて
