はじめに #
この記事は前編の続きである。作成したgeneratorクラスを使った時系列予測の方法を解説する。
学習データ #
図のように、 [-1, -1, 0, 0, 1, 1, 0, 0, …] を繰り返す時系列データが与えられたとき、次のステップの値を予測させる。 正しく予測するためには、最低でも3個以上の過去のデータを記憶する必要がある。
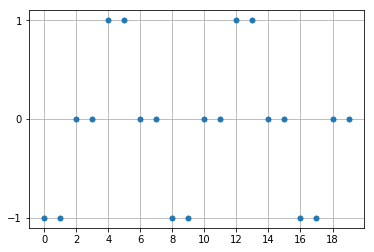
例えば、[0, 0]とデータが与えられても、次の値は1か-1か分からない。 さらに1ステップ前から[-1, 0, 0]と連続して初めて、次の値が1と予測できる。
説明変数x_setと目的変数y_setを以下のように作成する。
ここで、x_setとy_setは行数が等しい2次元配列であり、同じ行のデータは同じ時刻のデータである。
(実務で得られることが多いデータ形式であると思う)
x_base = np.array([-1,-1,0,0,1,1,0,0], dtype=np.float32).reshape(-1, 1)
x_set = np.empty([0, 1], dtype=np.float32)
for i in range(10):
x_set = np.vstack([x_set, x_base]) # 説明変数
y_set = x_set.copy() # 目的変数
学習 #
初めに、x_setとy_setを、自作した学習用ジェネレータReccurentTrainingGeneratorに与える。
ここで、batch_sizeは10, timestepsは5とした。
また、次のステップを予測するため、delayは1とした。
timesteps = 5
RTG = ReccurentTrainingGenerator(x_set, y_set, batch_size=10,
timesteps=timesteps, delay=1)
次に、ニューラルネットモデルを作成し、学習させる。
1層目はSimpleRNNレイヤ、2層目は全結合レイヤとする。ともにノード数は10である。
また、学習には通常のfitメソッドではなく、fit_generatorメソッドとして、引数にReccurentTrainingGeneratorオブジェクトをとる。
actfunc = "tanh"
model = Sequential()
model.add(SimpleRNN(10, activation=actfunc,
batch_input_shape=(None, timesteps, 1)))
model.add(Dense(10, activation=actfunc))
model.add(Dense(1))
model.compile(optimizer='sgd', loss='mean_squared_error')
history = model.fit_generator(RTG, epochs=20, verbose=1) # 学習する
予測 #
検証データとして、以下の配列x_testを与える。これに続くデータ(正解データ)は1である。
x_testをReccurentPredictingGeneratorクラスに与える。
予測には、通常のpredictメソッドではなく、predict_generatorメソッドを用いる。
x_test = np.array([-1,-1,0,0,1], dtype=np.float32).reshape(-1, 1)
# 検証データ
RPG = ReccurentPredictingGenerator(x_test, batch_size=1, timesteps=5)
# 予測用ジェネレータ
pred = model.predict_generator(RPG) # 予測する
print(pred)
実行結果
[[1.011917]]
予測値は1.012となり、正解(1)に近い値となった。
参考 #
前回と今回の記事のコードをまとめたものをGithubにおいている。 https://gist.github.com/helve2017/c20d6106a5dab00a8afa942584b60580
Kerasの公式リファレンス。 Sequentialモデル - Keras Documentation ユーティリティ - Keras Documentation
