はじめに #
ディープラーニング用のライブラリChainerの使い方を理解するため、ChainerのChainクラスとOptimizerを使って最小限のニューラルネットワーク (NN) を実装する。実装後、1次関数を学習させる。
環境 #
| ソフトウェア | バージョン |
|---|---|
| Spyder | 3.2.8 |
| Python | 3.6.5 |
| NumPy | 1.14.3 |
| Chainer | 4.2.0 |
以下では、各ライブラリを以下のようにインポートしていることを前提とする。
import numpy as np
import matplotlib.pyplot as plt
import chainer
import chainer.links as L
import chainer.functions as F
from chainer import optimizers, Chain
Chainクラスを使ったNNの構造定義 #
GPUで並列計算を行う場合などに再利用性を高めるため、NNの構造はクラスを定義して書かれることが多い。
例えば、2層のNNをMyChainクラスとして次のように記述する。
class MyChain(Chain):
def __init__(self):
super(MyChain, self).__init__()
with self.init_scope():
self.l1 = L.Linear(1, 2)
self.l2 = L.Linear(2, 1)
def __call__(self, x):
h = F.relu(self.l1(x))
return self.l2(h)
MyChainはChainerのChainクラスを親クラスとして継承している。
2行目の__init__関数は、MyChainクラスのオブジェクトが作成されるときに、実行される関数である。
6, 7行目のL.Linearは全結合層のクラスであり、第1引数は入力信号の数、第2引数は出力信号の数である。
8行目の__call__関数は、MyChainオブジェクトに引数を与えて呼び出すと、実行される関数である。ここでは、NNの順方向の計算を定義している。
Optimizer(最適化ルーチン) #
NNのパラメータを更新するには、optimizersオブジェクトを用いる。
以下に、実装の主要部分を示す。
def lossfun(train_y, pred_y):
loss = F.mean_squared_error(train_y, pred_y)
return loss
model = MyChain()
optimizer = optimizers.SGD()
optimizer.setup(model)
pred_y = model(train_x)
optimizer.update(lossfun, train_y, pred_y)
1~3行目のlossfunは、NNの学習に使用する損失関数である。ここでは、評価指標を教師データと推定値の二乗平均誤差 (Mean squared errors) としている。
次に、5~7行目で、MyChainオブジェクトを作成し、optimizersオブジェクトに渡している。ここでは、パラメータの更新規則は確率的勾配降下法 (SGD, stochastic gradient descent)とした。
9行目では、NNに説明変数train_xを渡して、予測値pred_yを得ている。
10行目では、optimizersのupdateメソッドに、評価関数lossfunとその引数(pred_yと目的変数の真値train_y)を渡して、modelのパラメータを更新している。
なお、updateに引数を渡さない方法もあるが、modelの勾配を消去する (cleargrads) 操作が必要になるため、今回は簡単なこちらの方法を用いた。
実装例 #
上記のMyChainクラスと、Optimizerを使って、実際に学習を行う。
ここでは、線形モデル y=x-5 を学習させる。
説明変数 x は0~9.9まで0.1刻みで100点とする。
また、教師データの目的変数には、平均0, 分散0.1の正規分布に従う信号をノイズとして加えた。
この教師データを100回反復させて学習させる(エポック数100)。
また、教師データを2点ずつ与えるバッチ処理を行う。
import numpy as np
import chainer
import chainer.links as L
import chainer.functions as F
from chainer import optimizers, Chain
import matplotlib.pyplot as plt
class MyChain(Chain):
def __init__(self):
super(MyChain, self).__init__()
with self.init_scope():
self.l1 = L.Linear(1, 2)
self.l2 = L.Linear(2, 1)
def __call__(self, x):
h = F.relu(self.l1(x))
return self.l2(h)
def lossfun(x, y):
loss = F.mean_squared_error(x, y)
return loss
np.random.seed(0)
model = MyChain()
x_data = np.arange(0, 10, 0.1, dtype=np.float32).reshape(-1,1)
x = chainer.Variable(x_data)
y = chainer.Variable(x_data-5)
optimizer = optimizers.SGD().setup(model)
n_epoch = 200
batch_size = 2
pred_y_before = model(x_data) # Prediction before learning
mean_err = []
for epoch in range(n_epoch):
err_temp = 0
for i in range(0, x.shape[0], batch_size):
train_y = y[i:i+batch_size]
train_x = x[i:i+batch_size]
pred_y = model(train_x)
optimizer.update(lossfun, train_y, pred_y)
err_temp += F.mean_squared_error(train_y, pred_y).data*batch_size
mean_err += [err_temp/x.shape[0]]
pred_y_after = model(x_data) # Prediction after learning
fig, ax = plt.subplots()
ax.plot(x_data.data, y.data, label="True values")
ax.plot(x_data.data, pred_y_before.data, label="Before learning")
ax.plot(x_data.data, pred_y_after.data, label="After learning")
ax.legend()
ax.grid()
plt.show()
fig, ax = plt.subplots()
ax.plot(mean_err)
ax.set_xlabel("Epoch")
ax.set_ylabel("Mean squared error")
ax.grid()
plt.show()
何もしなければL.Linearの重み行列Wは毎回ランダムに初期化されるため、np.random.seed(0)によって、Wの初期値を固定している。
また、mean_errには各エポックにおける予測値の二乗誤差平均を格納している。
学習前後のモデルの予測値は次のようになった(青が教師データ、黄色が学習前の予測値、緑が学習後の予測値)。学習によって、予測値が教師データに近づいている。
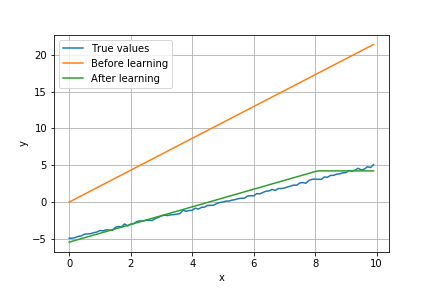
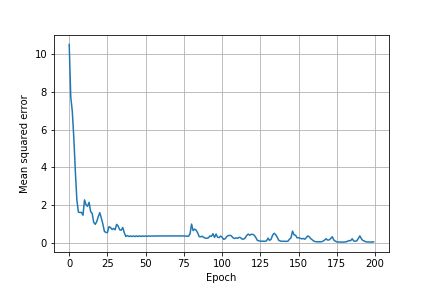
また、エポックごとの予測の二乗平均誤差は以下の通り。 時折増加しつつも、学習回数が増えるにつれて減少している。
参考リンク #
Creating Models — Chainer 7.7.0 documentation Optimizer — Chainer 7.7.0 documentation
