はじめに #
CasADiは自動微分と非線形最適化のためのライブラリである。C++で実装されており、C++, Python, Matlab, Octaveのインターフェースを備えている。 本記事ではPythonを使い、CasADiで非線形最適化問題を解く方法をまとめた。
CasADiにはIPOPTという非線形ソルバが含まれているため、これを用いる。IPOPTは主双対内点法を利用したソルバであり、大規模な非線形問題を高速に解くことができる。ただし、問題は連続である必要があり、大域的最適解を求めるには問題が凸である必要がある。
環境は以下の通り。
| ソフトウェア | バージョン |
|---|---|
| Python | 3.7.4 |
| CasADi | 3.5.5 |
ソフトウェアのインストール #
pipでCasADiをインストールする。CasADiには最適化ソルバも含まれており、同時にインストールされる。
pip install casadi
対象とする非線形計画問題 #
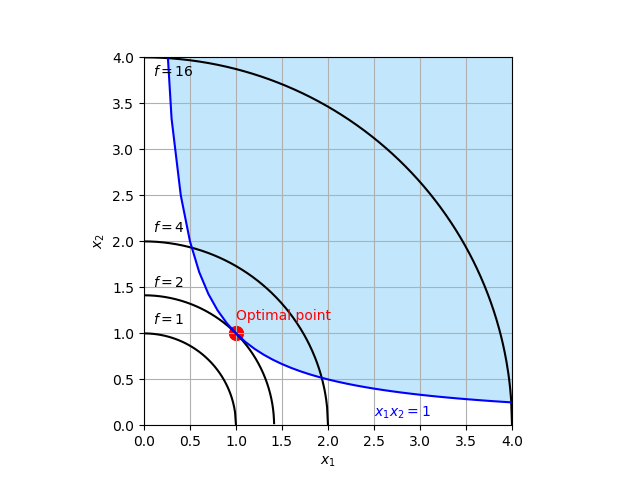
以下の制約付き非線形最小化問題を考える。
$$ \begin{array}{ll} \text{minimize} & f(x_1, x_2) = x_1^2 + x_2^2 \\\ \text{subject to} & x_1 x_2 \ge 1, \\\ & 0 \le x_1 \le 4, 0 \le x_2 \le 4 \end{array} $$図示すると以下のようになり、\((x_1, x_2)=(1, 1)\)で最小値\(2\)をとる。青色で図示した領域は実行可能領域を示す。
CasADiのソースコード #
上記の問題をCasADiを使って記述し、最適化を実行したコードは以下のようになる。
import casadi
opti = casadi.Opti()
# 変数を定義
x1 = opti.variable()
x2 = opti.variable()
# 初期値を指定
opti.set_initial(x1, 3)
opti.set_initial(x2, 3)
# 目的関数を定義
obj = x1**2 + x2**2
opti.minimize(obj)
# 制約条件を定義
opti.subject_to( x1*x2 >= 1 )
# 変数の範囲を定義
opti.subject_to( opti.bounded(0, x1, 4) )
opti.subject_to( opti.bounded(0, x2, 4) )
opti.solver('ipopt') # 最適化ソルバを設定
sol = opti.solve() # 最適化計算を実行
print(f'評価関数:{sol.value(obj)}')
print(f'x1: {sol.value(x1)}')
print(f'x2: {sol.value(x2)}')
実行結果は以下のようになり、最適値を得られている。
This is Ipopt version 3.12.3, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation).
(中略)
EXIT: Optimal Solution Found.
solver : t_proc (avg) t_wall (avg) n_eval
nlp_f | 0 ( 0) 0 ( 0) 19
nlp_g | 0 ( 0) 0 ( 0) 19
nlp_grad_f | 1.00ms ( 76.92us) 997.00us ( 76.69us) 13
nlp_hess_l | 0 ( 0) 0 ( 0) 11
nlp_jac_g | 0 ( 0) 0 ( 0) 13
total | 22.00ms ( 22.00ms) 21.94ms ( 21.94ms) 1
評価関数:1.9999999825046224
x1: 0.9999999956261556
x2: 0.9999999956261556
ソースコードの解説 #
以下、ソースコードの詳細を述べる。
最適化問題のオブジェクトの作成 #
まず、Optiクラスを用いて最適化問題のオブジェクトを作成する。
opti = casadi.Opti()
変数の定義 #
次に、opti.variable()メソッドを用いて変数を定義する。
x1 = opti.variable()
x2 = opti.variable()
variable()に引数を与えない場合、変数はスカラになる。一方、
x = opti.variable(2)
のように整数を引数にとることで、ベクトルにできる。
ベクトルにした場合、個々の要素にはx[0], x[1]のようにアクセスする。
初期値の指定 #
変数に初期値を指定する場合、opti.set_initial()メソッドを用いる。指定しない場合、初期値は0となる。
opti.set_initial(x1, 3)
opti.set_initial(x2, 3)
目的関数の定義 #
次に、目的関数を定義し、opti.minimize()メソッドに引数として与える。
obj = x1**2 + x2**2
opti.minimize(obj)
もしくは、以下のように目的関数を直接与えることも可能である。
opti.minimize(x1**2 + x2**2)
しかし、直接与えた場合、最適化後の目的関数の値を取得するには、以下のようにする必要があるため、目的関数を別途定義したほうが便利である。
sol.stats()['iterations']['obj'][-1]
制約条件の定義 #
subject_to()メソッドで制約条件を設定する。
opti.subject_to( x1*x2 >= 1 )
等式制約は==で、不等式制約は<=, >=, <, >でそれぞれ設定する。
また、制約式に上限と下限の両方がある場合、opti.bounded()メソッドでまとめて定義できる。例えば、\(1 \le x_1 x_2 \le 6\)という制約は以下のように定義できる。
opti.subject_to( opti.bounded(1 ,x1*x2, 6) )
変数の範囲の指定 #
opti.subject_to()メソッドとopti.bounded()メソッドを用いて、変数の範囲(下限値と上限値)を指定できる。
opti.subject_to( opti.bounded(0, x1, 4) )
opti.subject_to( opti.bounded(0, x2, 4) )
ソルバの指定と最適化 #
最後に、ソルバを指定して最適化を行う。
opti.solver('ipopt') # 最適化ソルバを設定
sol = opti.solve() # 最適化計算を実行
solverメソッドでソルバを指定する。ここではIPOPTを用いる。次に、solveメソッドを実行すると、最適化が行われる。solには最適化の結果が格納される。
最適化ソルバのオプション設定 #
最適化ソルバ(ここではIPOPT)にオプションを設定するためには、solverメソッドに辞書形式で渡す。
ここで、solverメソッドの2番目の引数はCasADiプラグインのオプション(本記事では説明を省略)、3番目の引数が最適化ソルバのオプションになる。
p_opts = {}
s_opts = {'print_level' : 4,
'tol' : 1E-3}
opti.solver('ipopt', p_opts, s_opts)
sol = opti.solve()
この例では以下のように設定した。
- 最適化計算のログ出力の詳細度合い (
print_level) を4(0~12の範囲。数字が大きいほど詳細になる) - 最適解の許容誤差 (
tol) を1E-3
IPOPTで設定可能なオプションについては以下のページを参照。
一覧の形式で確認したい場合には以下のページを参照。
最適化結果の評価 #
最適化後の変数や目的関数の値を取得するには、solのvalueメソッドに変数名を渡す。
>>> sol.value(obj)
1.9999999825046224
>>> sol.value(x1)
0.9999999956261556
>>> sol.value(x2)
0.9999999956261556
最適化問題の概要を表示するには、sol.disp(), sol.stats()などを実行する。
>>> sol.disp()
Opti {
instance #7
#variables: 2 (nx = 2)
#parameters: 0 (np = 0)
#constraints: 3 (ng = 3)
CasADi solver allocated.
CasADi solver was called: Solve_Succeeded
}
>>> sol.stats()
{'iter_count': 11,
'iterations': {'alpha_du': [0.0,
1.0,
0.00011355335462534469,
(中略)
't_wall_nlp_jac_g': 0.0,
't_wall_total': 0.011968,
'unified_return_status': 'SOLVER_RET_UNKNOWN'}
参考 #
CasADiの公式リファレンス
