↓ メインコンテンツへスキップ

PythonとCasADiを使ったDirect Single Shooting法による最適制御

·2545 文字·6 分
Python CasADi 最適化
目次

はじめに
#

Pythonと最適化ライブラリCasADiを使って、Direct Single Shooting法と呼ばれる手法によって最適制御問題を解きました。対象とした例題は斜方投射（物体を斜め方向に上げる）で、指定の時刻・距離に物体を到達させる最小の初速度を求めます。

Direct Single Shooting法は以下の特徴を持つ最適制御手法です。

  • 制御の開始から終了まで、時刻を\(t_0, t_1, ..., t_f\)と（等間隔に）分割する
  • 分割された時刻ごとに、その時間幅内で入力\(u(t)\)の値は一定とする
  • 時間幅ごとに状態\(x(t)\)を数値積分により求める

CasADiとDirect Single Shooting法に関する詳細は、それぞれ以下の記事を参考にしてください。

この記事で使用したPythonとライブラリのバージョンは以下の通りです。

ソフトウェア バージョン
Python 3.8.8
NumPy 1.20.1
CasADi 3.5.5
IPOPT 3.12.3
Matplotlib 3.3.4

CasADiとIPOPTがインストールされていない場合、以下でインストールします。

pip install casadi
pip install ipopt

斜方投射の運動方程式
#

まず、斜方投射の運動方程式を示します。斜方投射は、物体に初速度を与えて空中に投げ上げる運動のことです。

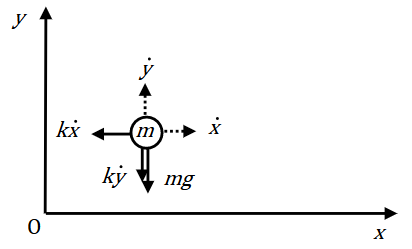
斜方投射の開始点を原点として、水平方向に\(x\)軸、鉛直方向に\(y\)軸をとります。物体の質量を\(m\)とします。また、物体には速度に比例した空気抵抗が働くとして、その係数を\(k(>0)\)とします。

このとき、\(x\)方向と\(y\)方向の運動方程式は、それぞれ以下のようになります。

$$m \ddot{x} + k \dot{x} = 0 \\\ m \ddot{y} + k \dot{y} + mg = 0$$

ただし、\(g\)は重力加速度です。

projectile motion
projectile motion

次に、CasADiで運動方程式を扱えるように、\(\dot{z}=f(z)\)という1階微分方程式の形に式を変形します。 ここで、

$$z=[x, y, \dot{x}, \dot{y}]^\top$$

とおくと、運動方程式は以下のようになります。

$$\dot{z} = \left[ \begin{array}{c} \dot{x} \\\ \dot{y} \\\ -\frac{k}{m}\dot{x} \\\ -\frac{k}{m}\dot{y} -g \end{array} \right] $$

斜方投射のPythonコード
#

斜方投射をCasADiを使って解く、Pythonコードを示します。

斜方投射のパラメータと微分方程式モデル
#

まず、斜方投射のパラメータと微分方程式モデルを設定します。

import numpy as np
import casadi as ca
import matplotlib.pyplot as plt

Ts = 1.0 # サンプリング周期[s]
N = 10 # サンプリング点数

m = 1 # 質量[kg]
k = 0.5 # 空気抵抗係数[(N・s)/m]
g = 9.81 # 重力加速度[m/(s^2)]

# 斜方投射を微分方程式で記述する
z = ca.MX.sym('z', 4) # x, y, x_dot, y_dot
zdot = ca.vertcat(z[2], z[3], -k/m*z[2], -k/m*z[3]-g)

dae = {'x':z, 
       'ode':zdot}
opts = {'tf':Ts}
F = ca.integrator('F', 'cvodes', dae, opts)

サンプリング周期を1[s], サンプリング点数をN=10とするので、シミュレーション全体の時間は10秒です。また、物体の質量と空気抵抗は適当な値としています。 optsのtfには、微分方程式を実行する時間を指定しています。

最適化問題の定式化
#

次に、最適化問題を定式化します。

u = ca.MX.sym('U', 2) # x, y方向の初速[m/s]

Xk = ca.vertcat(ca.MX([0, 0]), u)
for i in range(N):
    Fk = F(x0=Xk) # Tsだけ斜方投射をシミュレーションする（微分方程式を解く）
    Xk = Fk['xf']

J = ca.sum1(u**2) # 目的関数
prob = {'f': J, 'x': u, 'g': Xk[:2]}
solver = ca.nlpsol('solver', 'ipopt', prob)
sol = solver(x0=[1, 1], lbx=[0, 0], ubx=[ca.inf, ca.inf], 
             lbg=[100, 0], ubg=[100, 0])

uは最適化問題の未知変数ベクトルで、x, y方向の初速になります。 その次のfor文の内側で、サンプリング周期Tsだけ斜方投射の微分方程式を解くことをN回だけ繰り返します。

目的関数Jは、速度エネルギーを最小化すること、すなわち\(\dot{x}_0^2 + \dot{y}_0^2\)とします。

また、未知変数ベクトルuの初期値はx0=[1, 1]とし、下限値をlbx=[0, 0], 上限値をubx=[ca.inf, ca.inf]としています。

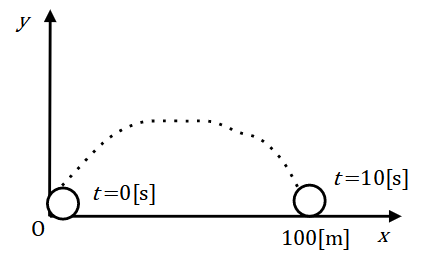
さらに、最終時刻t=10[s]に物体がx=100[m], y=0[m]の位置にあるものとします。これは制約'g': Xk[:2]として最終時刻の位置をとり、下限値lbg=[100, 0], 上限値ubg=[100, 0]で与えます。

また、最適化問題を解くために非線形ソルバIPOPTを使用しています。

projectile problem
projectile problem

ここまでのコードを実行すると、以下のログが表示され、最適化問題を解くことができます。 実行時間は78.15msでした。

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
 Ipopt is released as open source code under the Eclipse Public License (EPL).
         For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************

This is Ipopt version 3.12.3, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation).

Number of nonzeros in equality constraint Jacobian...:        2
Number of nonzeros in inequality constraint Jacobian.:        0
Number of nonzeros in Lagrangian Hessian.............:        2

Total number of variables............................:        2
                     variables with only lower bounds:        2
                variables with lower and upper bounds:        0
                     variables with only upper bounds:        0
Total number of equality constraints.................:        2
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0 2.0000000e+000 1.55e+002 1.00e+000  -1.0 0.00e+000    -  0.00e+000 0.00e+000   0
   1 8.7980408e+003 2.78e-005 7.81e+001  -1.0 7.81e+001    -  1.25e-002 1.00e+000h  1
   2 8.7980379e+003 3.86e-010 1.72e-003  -1.0 1.40e-005    -  9.95e-001 1.00e+000h  1

Number of Iterations....: 2

                                   (scaled)                 (unscaled)
Objective...............:  8.7980378964751490e+003   8.7980378964751490e+003
Dual infeasibility......:  1.4210854715202004e-014   1.4210854715202004e-014
Constraint violation....:  3.8573360205111218e-010   3.8573360205111218e-010
Complementarity.........:  0.0000000000000000e+000   0.0000000000000000e+000
Overall NLP error.......:  3.8573360205111218e-010   3.8573360205111218e-010


Number of objective function evaluations             = 3
Number of objective gradient evaluations             = 3
Number of equality constraint evaluations            = 3
Number of inequality constraint evaluations          = 0
Number of equality constraint Jacobian evaluations   = 3
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations             = 2
Total CPU secs in IPOPT (w/o function evaluations)   =      0.016
Total CPU secs in NLP function evaluations           =      0.046

EXIT: Optimal Solution Found.
      solver  :   t_proc      (avg)   t_wall      (avg)    n_eval
       nlp_f  |        0 (       0)        0 (       0)         3
       nlp_g  |  16.00ms (  5.33ms)  15.60ms (  5.20ms)         3
  nlp_grad_f  |        0 (       0)        0 (       0)         4
  nlp_hess_l  |  30.00ms ( 15.00ms)  31.33ms ( 15.67ms)         2
   nlp_jac_g  |        0 (       0)        0 (       0)         4
       total  |  78.00ms ( 78.00ms)  78.15ms ( 78.15ms)         1

また、最適解を表示します。

u_opt = sol['x']
print(u_opt)

実行結果
# 

[50.3392, 79.1455]

すなわち、\(x, y\)軸方向の初速はそれぞれ50.3[m/s], 79.1[m/s]となりました。

最適化結果のプロット
#

最後に最適化結果をプロットします。

最適化問題を定式化したときと同様に、斜方投射の微分方程式をサンプリング周期Tsだけ解くことをN回繰り返し、位置と速度のベクトル\(z\)の時刻歴データz_historyを得ます。

z_history = [[0, 0] + u_opt.toarray().flatten().tolist()]
for i in range(N):
    Fk = F(x0=z_history[-1])
    z_history += [Fk['xf'].toarray().flatten().tolist()]

z_history = np.array(z_history)
time = np.arange(0, N+Ts, Ts)

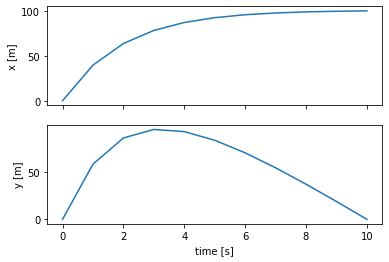
まず、物体の位置\(x, y\)の時刻歴データをプロットします。時刻10[s]で、物体はx=100[m], y=0[m]に到達していることが分かります。

fig, ax = plt.subplots(nrows=2, sharex=True)
ax[0].plot(time, z_history[:, 0])
ax[0].set_ylabel('x [m]')
ax[1].plot(time, z_history[:, 1])
ax[1].set_xlabel('time [s]')
ax[1].set_ylabel('y [m]')
plt.show()

projectile solution
projectile solution

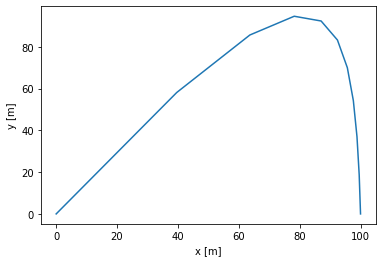
最後に、x-y平面に物体の軌跡をプロットします。空気抵抗があるため、綺麗な放物線とはなっていません。

fig, ax = plt.subplots()
ax.plot(z_history[:, 0], z_history[:, 1])
ax.set_xlabel('x [m]')
ax.set_ylabel('y [m]')
plt.show()

projectile trajectory solution
projectile trajectory solution

まとめ
#

PythonとCasADiを使って、斜方投射を例題として、与えられた時刻と位置に物体を到達させるために必要なエネルギー（初速）を最小化しました。手法にはDirect Single Shooting法を用いました。

参考
#

CasADiの公式リファレンス

Helve
著者
Helve
関西在住、電機メーカ勤務のエンジニア。X（旧Twitter）で新着記事を配信中です

関連記事

最適制御向け最適化ライブラリOpEnに入門する
··1759 文字·4 分
Python OpEn CasADi 最適化
Rust製の最適制御向け最適化ライブラリOpEnに入門するためチュートリアルの非線形計画問題を解いたので、備忘録を兼ねてまとめた。
CasADiとBONMINで混合整数非線形計画問題を解く
·913 文字·2 分
Python CasADi 最適化
Pythonで自動微分・非線形最適化ライブラリCasADiと最適化ソルバBONMINを使って、混合整数非線形計画問題を解く方法をまとめた。
CasADiとIPOPTで非線形計画問題を解く
··2122 文字·5 分
Python CasADi 最適化
Pythonで自動微分・非線形最適化ライブラリCasADiと最適化ソルバIPOPTを使って、制約付き非線形計画問題を解く方法をまとめた。
PythonとCasADiで常微分方程式を解く
·1228 文字·3 分
Python CasADi 微分方程式
Pythonと自動微分・最適化ライブラリCasADiを使って、常微分方程式解く方法をまとめた。
Rust製最適化ライブラリOpEnのインストール
··868 文字·2 分
Python OpEn 最適化
Rust製の最適化ライブラリOpEnをWindows 10にインストールし、Pythonから使えるようにする。
Pyomoの変数をベクトル化する
·1409 文字·3 分
Python Pyomo 最適化
Pyomoで多変数の最適化を簡潔に記述するため、変数をベクトル化する方法をまとめた。