はじめに #
本記事では、BFGS公式の準ニュートン法について簡単に解説し、Pythonで実装した例を示す。実装は、数理工学社の「工学基礎 最適化とその応用」の4.8節「準ニュートン法」を参考にさせていただいた。
準ニュートン法は、再急降下法とニュートン法の両者の長所を持つような手法である。再急降下法は、収束速度が1次でしかない替わりに、初期点が解から離れていても収束する(大域的収束性)。一方、ニュートン法は、解近傍の収束速度は2次であるが、探索方向が評価関数の勾配方向と一致するとは限らないため、直線探索をそのまま利用できない。 両者の実装については、それぞれ以下の記事を参考。
本記事で使用したPythonとライブラリのバージョンは以下の通り。
| バージョン | |
|---|---|
| Python | 3.8.5 |
| NumPy | 1.19.2 |
| matplotlib | 3.3.2 |
実装では、以下のようにライブラリをインポートしていることを前提とする。
import numpy as np
import matplotlib.pyplot as plt
準ニュートン法 #
概要 #
最小化したい関数を\(f(\bm{x})\)とする。 ニュートン法の\(k\)回目の更新において、解の更新方向\(\bm{d}_k\)は次の方程式の解として与えられる。
$$ \nabla ^2 f(\bm{x}_k) \bm{d}_k = - \nabla f(\bm{x}_k) $$しかし、一般にヘッセ行列\(\nabla ^2 f(\bm{x}_k)\)が正定値である保証はない。したがって、ヘッセ行列は逆行列を持たない可能性があり、上記の方程式を\(\bm{d}_k\)について解けるとは限らない。
そこで、準ニュートン法ではヘッセ行列を適当な正定値行列で近似する。準ニュートン法には、ヘッセ行列を近似する方法と、ヘッセ行列の逆行列を近似する方法の2つがある。この記事では前者について述べる。
ヘッセ行列を近似する正定値行列を\(B_k\)として、解の更新方向\(\bm{d}_k\)を次の方程式の解として求める。
$$ B_k \bm{d} = - \nabla f(\bm{x}_k) $$\(B_k\)を求めるには、勾配\(\nabla f(\bm{x})\)のテイラー展開(次式)を利用する。
$$ \nabla f(\bm{x}_k) = \nabla f(\bm{x}\_{k+1}) + \nabla^2 f(\bm{x}\_{k+1}) (\bm{x}_k - \bm{x}\_{k+1}) + ... $$すなわち、以下の近似式が成り立つ。
$$ \nabla^2 f(\bm{x}\_{k+1}) (\bm{x}\_{k+1} - \bm{x}_k) \approx \nabla f(\bm{x}\_{k+1}) - \nabla f(\bm{x}_k) $$さらに、
$$ \bm{s}_k = \bm{x}\_{k+1} - \bm{x}_k, \\ \bm{y}_k = \nabla f(\bm{x}\_{k+1}) - \nabla f(\bm{x}_k) $$と置き、以下を満たすように近似行列\(B_{k+1}\)を求める。
$$ B_{k+1} \bm{s}_k = \bm{y}_k $$この式をセカント条件と呼ぶ。
ヘッセ行列を近似する方法の1つとして、BFGS (Broyden–Fletcher–Goldfarb–Shanno) 法がある。この方法では、以下の公式を用いて近似行列を更新する。
$$ B_{k+1} = B_k - \frac{B_k \bm{s} (B_k \bm{s}_k)^\top}{\bm{s}_k^\top B_k \bm{s}_k} + \frac{\bm{y}_k \bm{y}_k^\top}{\bm{s}_k^\top \bm{y}_k } $$初期行列\(B_0\)には通常は単位行列が用いられてる。
アルゴリズム #
準ニュートン法のアルゴリズムは以下のようになる。
- 解の初期値\(x_0\), 初期行列\(B_0\)を用意
- \(B_k \bm{d}_k = - \nabla f(\bm{x}_k)\)を解いて解の更新方向\(\bm{d}_k\)を求める
- 直線探索によりステップ幅\(\alpha_k\)を求める
- \(\bm{x}\_{k+1} = \bm{x}_k + \alpha_k \bm{d}_k\)で解を更新
- BFGS公式で近似行列\(B\)を更新
解が収束するか、反復回数の上限に達するまで、上記のアルゴリズム2~5を繰り返す。
Pythonによる実装 #
BFGS公式を用いた準ニュートン法をPythonで実装した。 直線探索にはArmijo条件を用いた。
目的関数 #
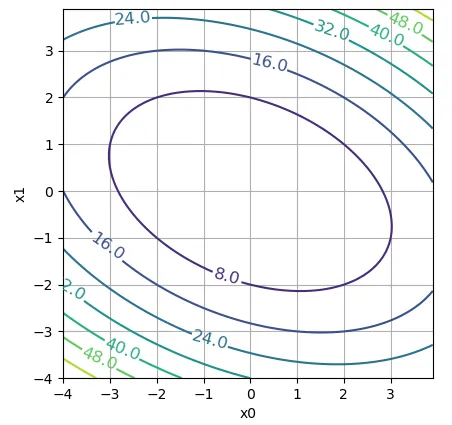
以下の評価関数を考える。
$$ f(\bm{x}) = 2x_0^2 + x_0 x_1 + x_1^2 $$この関数は\((x_1, x_2)=(0, 0)\)で最小値0をとる。また、勾配ベクトルは次式となる。
$$ \nabla f(\bm{x}) = \begin{bmatrix} 4x_0 + x_1 \\ x_0 + 2x_1 \end{bmatrix} $$評価関数と勾配ベクトルを返す関数を以下のように定義する。
def obj_func(x):
"""評価関数"""
return 2*x[0]**2 + x[1]**2 + x[0]*x[1]
def obj_grad(x):
"""評価関数の勾配"""
return np.array([4*x[0] + x[1], x[0] + 2*x[1]])
評価関数のプロットを示す。
x0 = np.arange(-4, 4, 0.1)
x1 = np.arange(-4, 4, 0.1)
X0, X1 = np.meshgrid(x0, x1)
Y = obj_func(np.dstack((X0,X1)).T)
fig, ax = plt.subplots()
contourSet = ax.contour(X0, X1, Y)
ax.clabel(contourSet, fontsize=12, fmt="%.1f")
ax.set_xlabel("x0")
ax.set_ylabel("x1")
ax.set_aspect('equal')
ax.grid()
plt.show()
準ニュートン法 #
準ニュートン法のアルゴリズムを以下に示す。 解の初期値を\((3, 3)\), 反復回数を10回とした。
x = [3, 3]
B = np.eye(len(x)) # ヘッセ行列の近似行列
tau = 0.9 # 直線探索のパラメータ
xi = 0.3 # 直線探索のパラメータ
grad = obj_grad(x)
for i in range(10):
f = obj_func(x)
d = - np.dot(np.linalg.inv(B), grad) # 探索方向
# Armijo条件を用いた直線探索
alpha = 1
temp = xi*np.dot(grad, d)
while obj_func(x+alpha*d) > f+alpha*temp:
alpha *= tau
x += alpha*d # 解の更新
old_grad = grad
grad = obj_grad(x)
s = (alpha*d).reshape([-1,1]) # 解の変化量
y = (grad - old_grad).reshape([-1,1]) # 勾配の変化量
Bs = np.dot(B, s)
B -= (Bs*Bs.T)/np.dot(s.T, Bs) - (y*y.T)/np.dot(s.T, y)
# ヘッセ行列の近似行列を更新
print(x)
# print(B)
実行結果 #
解の推移を以下に示す。最適解\((0, 0)\)に収束していることが分かる。
[-1.70715894 0.17570464]
[ 0.27118335 -0.56701972]
[-0.01360106 0.19786906]
[-0.00424114 -0.0012749 ]
[ 0.00027077 -0.00011258]
[-7.12942645e-07 2.00328906e-06]
[ 7.26783781e-10 -1.66812385e-08]
[8.90466726e-12 2.23457180e-12]
[-1.38353745e-14 5.85295723e-15]
[ 8.89368462e-19 -2.52015868e-18]
また、近似行列Bの反復1, 5, 10回目の値はそれぞれ以下の通り。
1回目
[[3.83903021 1.26828299]
[1.26828299 1.55286169]]
5回目
[[3.99881539 1.00459841]
[1.00459841 1.98214989]]
10回目
[[3.9999154 0.9998001 ]
[0.9998001 1.99952763]]
実際に評価関数のヘッセ行列を計算すると、以下のようになる。
$$ \nabla^2 f(\bm{x}) = \begin{bmatrix} 4 & 1 \\\ 1 & 2 \end{bmatrix} $$反復回数が増えるにつれて、実際のヘッセ行列の値に近づいている。
参考 #
準ニュートン法の詳細なアルゴリスムについては、以下の書籍を参考とした。
