はじめに #
本記事では、線形計画問題に対する主双対内点法 (primal-dual interior point method) についてまとめた。
内点法 #
主双対内点法の前に内点法 (interior point method) について述べる。 内点法とは、線形計画問題を多項式時間で解くことが可能な手法である。
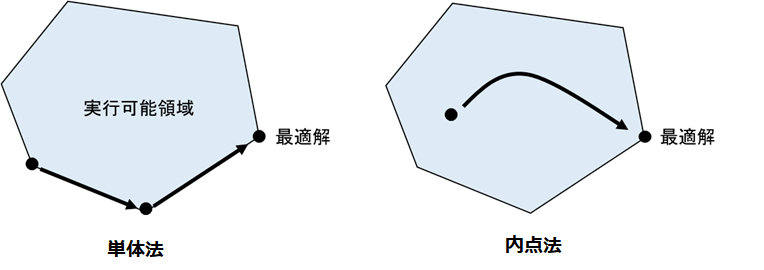
線形計画問題を解く手法として、単体法 (simplex method) と呼ばれるものもある。 線形計画問題では、最適解は実行可能領域の端点にあることが知られている。 単体法では実行可能領域の端点を移動することで、有限回の反復で厳密な最適解が探索される。 単体法は一般的な線形計画問題に対して有用な手法であるが、問題が特殊な場合には反復回数が指数関数的に増加する。
一方、内点法は実行可能領域の内部を最適解に向けて探索する手法である。 内点法では問題の規模に対して計算時間が多項式的にしか増加しない。 そのため、大規模な問題に対しては内点法が適している。
主双対内点法 #
主双対内点法は、双対定理を利用して、線形計画問題の主問題と双対問題を同時に解く手法である。
主問題または双対問題を単独に内点法で解く手法もあるが、主双対内点法はそれらの手法よりも計算が速いという利点がある。 また、詳細は本記事では触れないが、主双対内点法は非線形問題にも適用できる。
主双対内点法のアルゴリズム #
最適性条件 #
双対定理を用いて、線形計画問題の最適解が満たす条件(最適性条件)を考える。 双対定理については以下の記事も参考のこと。
まず、以下の制約付き線形計画問題を考える。
$$ \mathrm{min} \ f_p(\boldsymbol{x}) = \boldsymbol{c}^{\top} \boldsymbol{x} \\ \mathrm{s.t.}\ A\boldsymbol{x}=\boldsymbol{b}, \boldsymbol{x} \ge \boldsymbol{0} $$ここで、\( \boldsymbol{x} \in \mathbb{R}^n, A\in \mathbb{R}^{n\times m}, \boldsymbol{b} \in \mathbb{R}^m, \boldsymbol{c} \in \mathbb{R}^n\)である。
この問題に対して、双対問題 (dual problem) は以下で与えられる。
$$ \mathrm{max} \ f_d(\boldsymbol{y}) = \boldsymbol{b}^{\top} \boldsymbol{y} \\ \mathrm{s.t.}\ A^{\top} \boldsymbol{y}+\boldsymbol{z} =\boldsymbol{c}, \boldsymbol{z} \ge \boldsymbol{0} $$ここで、\( \boldsymbol{y} \in \mathbb{R}^m, \boldsymbol{z} \in \mathbb{R}^m\)である。
双対問題に対し、元の問題を主問題 (primal problem) と呼ぶ。 双対定理により、主問題と双対問題が最適解を持つならば、2つの最適解の値は一致する。 すなわち、
$$ \boldsymbol{c}^{\top} \boldsymbol{x} = \boldsymbol{b}^{\top} \boldsymbol{y} $$である。 この式を変形すると、
$$ \begin{array}{rl} \boldsymbol{c}^{\top} \boldsymbol{x} - \boldsymbol{b}^{\top} \boldsymbol{y} = 0 & \Leftrightarrow (A^{\top} \boldsymbol{y}+\boldsymbol{z})^{\top} \boldsymbol{x} - (A\boldsymbol{x})^{\top} \boldsymbol{y} = 0 \\\ & \Leftrightarrow \boldsymbol{z}^{\top} \boldsymbol{x} = 0 \\\ & \Leftrightarrow x_i z_i = 0 (i=1, ..., n) \\\ & \Leftrightarrow X \boldsymbol{z} = \boldsymbol{0} \end{array} $$が得られる。 ただし、\(X\)は対角が\(x_i (i=1, ..., n)\), その他の要素が0の行列である。
したがって、最適性条件は以下のようになる。
$$ \begin{array}{rl} \left( \begin{array}{l} A\boldsymbol{x}=\boldsymbol{b} \\ A^{\top} \boldsymbol{y}+\boldsymbol{z} =\boldsymbol{c} \\ X \boldsymbol{z} = \boldsymbol{0} \\ \boldsymbol{x} \ge \boldsymbol{0}, \boldsymbol{z} \ge \boldsymbol{0} \end{array} \right. \end{array} $$1番目と2番目の条件は、それぞれ主問題と双対問題の制約条件である。 3番目の条件は、双対定理より得られた条件である。
最適性条件を以下のベクトル表現に変形する。
$$ \boldsymbol{r_0}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) = \left[ \begin{array}{c} A \boldsymbol{x} - \boldsymbol{b} \\ A^{\top} \boldsymbol{y} + \boldsymbol{z} - \boldsymbol{c} \\ X \boldsymbol{z} \end{array} \right] = \boldsymbol{0} \\ \boldsymbol{x} \ge \boldsymbol{0}, \boldsymbol{z} \ge \boldsymbol{0} $$すなわち、最適解は\(\boldsymbol{r_0}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) = \boldsymbol{0}\)を満たす\(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}\)である。
上記の方程式は非線形であるため、最適解を直接求めることは困難である。 よって、ニュートン法により解候補を徐々に最適解の方向に更新することによって最適解を求める。
解の更新 #
解の更新方向を\([\boldsymbol{\Delta x}, \boldsymbol{\Delta y}, \boldsymbol{\Delta z}]\)とすると、これを求めるには、次の1次方程式を解けばよい。
$$ J(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) \left[ \begin{array}{c} \boldsymbol{\Delta x} \\ \boldsymbol{\Delta y} \\ \boldsymbol{\Delta z} \end{array} \right] = - \boldsymbol{r_0}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) $$ここで、\(J(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z})\)は\(\boldsymbol{r_0}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z})\)のヤコビ行列であり、
$$ J(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) = \left[ \begin{array}{ccc} O & A^{\top} & I \\ A & O & O \\ Z & O & X \end{array} \right] $$で与えられる。 \(Z\)は対角が\(z_i (i=1, ..., n)\)でその他の要素が0の行列、\(I\)は単位行列である。
解の探索方向が求まれば、適当なステップサイズ\(\alpha > 0\)により、解を以下のように更新する。
$$ \left[ \begin{array}{c} \boldsymbol{x_{k+1}} \\ \boldsymbol{y_{k+1}} \\ \boldsymbol{z_{k+1}} \\ \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{x_{k}} \\ \boldsymbol{y_{k}} \\ \boldsymbol{z_{k}} \\ \end{array} \right] + \alpha \left[ \begin{array}{c} \boldsymbol{\Delta x} \\ \boldsymbol{\Delta y} \\ \boldsymbol{\Delta z} \\ \end{array} \right] $$ただし、\(k\)は更新回数を示す。
以上が主双対内点法の基本的なアルゴリズムであるが、実際には収束性を改善するため様々な工夫がなされている。 パス追跡法、アフィン・スケーリング法、プレディクタ・コレクタ法など様々な手法があるが、以下ではパス追跡法について述べる。
パス追跡法 #
解の更新時に非負制約\(\boldsymbol{x} \ge \boldsymbol{0}, \boldsymbol{z} \ge \boldsymbol{0}\)の境界に近づくと、最適解への収束が停滞する可能性がある。 したがって、最適解への収束速度を上げるためには、可能な限り境界から遠い場所を通る必要がある。
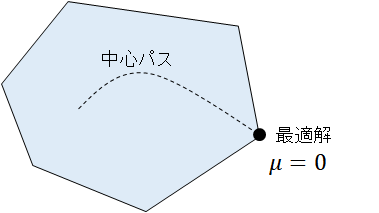
そこで、中心パス (central path) と呼ばれるものを考える。 パラメータ\(\mu >0\)を導入し、最適性条件の方程式を以下のように置き換える。
$$ \boldsymbol{r}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) = \left[ \begin{array}{c} A\boldsymbol{x} - \boldsymbol{b} \\ A^{\top} \boldsymbol{y}+\boldsymbol{z} - \boldsymbol{c} \\ X \boldsymbol{z} - \mu \boldsymbol{e} \end{array} \right] = \boldsymbol{0} $$$$ \boldsymbol{x} \ge \boldsymbol{0}, \boldsymbol{z} \ge \boldsymbol{0} $$
ここで、\(\boldsymbol{e}\)は要素が全て1のベクトルである。 \( X \boldsymbol{z} = \mu \boldsymbol{e}\)とすることで、\(x_i, z_i (i=0, ..., n)\)が0に近づかないようにしている。
\(\mu\)の値を固定したとき、上記の方程式はただ1つの解を持つ。 この解は、\(\mu\)の値を変化させると滑らかな曲線を描き、\(\mu = 0\)となるときに最適解となる。 したがって、解を更新しながら\(\mu\)の値を徐々に小さくすることにより、最適解に収束することが期待できる。
参考 #
以下の論文を参考にさせて頂いた。
