はじめに #
2次元極座標系における衛星・惑星の軌道をPythonでシミュレートします。
この記事では、2次元極座標系における運動方程式を示した後、円軌道とモルニア軌道(楕円軌道)のシミュレーションを行うPythonコードを示します。
Pythonライブラリのバージョンは以下の通りです。
| ライブラリ | バージョン |
|---|---|
| Python | 3.9.7 |
| SciPy | 1.7.1 |
| Matplotlib | 3.4.3 |
極座標系の運動方程式 #
中心となる天体を極座標系の原点にとり、もう1つの天体との距離を\(r\), 角度を\(\theta\)とします。また、それぞれの天体の質量を\(M\), \(m\)とします。さらに、中心でない天体に作用する力を\(F_r\), \(F_{\theta}\)とします。
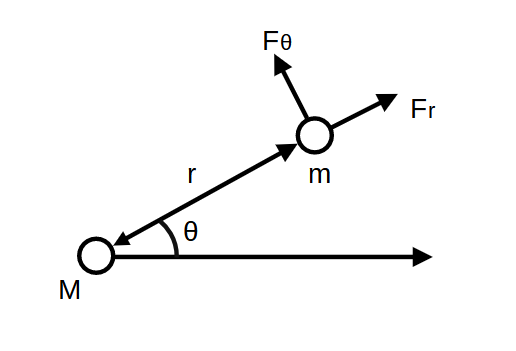
極座標系の運動方程式は以下になります。
$$m(\ddot{r} - r \dot{\theta}^2) = F_r \\ m \frac{1}{r} \frac{d}{dt}(r^2 \dot{\theta}) = F_{\theta}$$これを加速度\(\ddot{r}\), 角加速度\(\ddot{\theta}\)について解くと、以下のようになります。
$$ \ddot{r} = \frac{1}{m} F_r + r \dot{\theta}^2 \\ \ddot{\theta} = \frac{1}{r} \left( \frac{F_{\theta}}{m} - 2\dot{r}\dot{\theta} \right) $$さらに、速度を\(v:=\dot{r}\), 角速度を\(\omega:=\dot{\theta}\)と定義します。さらに、\(x=[r, \theta, v, \omega]^\top\)とおくと、運動方程式は以下に変形できます。
$$ \dot{x} = \begin{bmatrix} v \\ \omega \\ \frac{1}{m} F_r + r \dot{\theta}^2 \\ \frac{1}{r} \left( \frac{F_{\theta}}{m} - 2\dot{r}\dot{\theta} \right) \end{bmatrix} $$また、天体に作用する力は重力のみであるため、
$$ F_r = - G\frac{Mm}{r^2} \\\ F_{\theta} = 0$$となります。ただし、\(G\)は重力定数です。
Pythonによるシミュレーション #
前節で求めた運動方程式を使って、Pythonによるシミュレーションを行います。SciPyのsolve_ivpという微分方程式を解く関数を利用します。
ここでは、地球を中心として周回する衛星の軌道をシミュレーションします。パラメータを以下の表に示します。
| パラメータ | 記号 | 値 |
|---|---|---|
| 地球半径 | Re |
6378e3 [m] |
| 重力定数 | G |
6.674e-11 [m3/kg/s2] |
| 地球質量 | M |
5.9724e24 [kg] |
シミュレーションする軌道は、地上からの高度500 [km]の円軌道、およびモルニア軌道と呼ばれる周期12時間の楕円軌道の2つです。
2つのシミュレーションではパラメータや運動方程式の関数orbit()は共通であり、以下のように定義します。
import math
import numpy as np
from scipy.integrate import solve_ivp
from matplotlib import pyplot as plt
Re = 6378e3 # radius of Earth [m]
G = 6.674e-11 # constant of gravitation [m3/kg/s2]
M = 5.9724e24 # Earth mass [kg]
GMe = G*M
m = 100 # [kg]
def orbit(t, x):
r, theta, v, omega = x
Fr = -GMe*m/r**2
Ftheta = 0
return [v, omega, Fr/m + r*omega**2, (Ftheta/m - 2*v*omega)/r]
円軌道 #
地上からの高度500[km]の円軌道では、速度7612 [m/s], 周期5640 [秒](94 [分])です。\(r\), \(\theta\)軸方向の初期位置をそれぞれ6878 [km] (=500+6378 [km] ), 0 [rad]とします。また、初期角速度は0.0011068 [rad/s] (=7612 [m/s] /6878e3 [m] )となります。
以下のようにパラメータを定義し、運動方程式をsolve_ivp()関数で解きます。
# 円軌道
r0 = 500e3 + Re # init [m]
v0 = 7.6126e3 # [m/s]
omega0 = v0/r0 # [rad/s]
x_init = [r0, 0, 0, omega0]
sol = solve_ivp(orbit, [0, 5640], x_init)
以下のコードでシミュレーション結果をプロットします。
r_sol = sol.y[0]
theta_sol = sol.y[1]
fig = plt.figure(figsize=(4, 4))
ax = fig.add_subplot(111, projection="polar")
ax.plot(theta_sol, r_sol, "o")
ax.set_rlim(0, 8e6)
plt.show()
fig, ax = plt.subplots(nrows=2, sharex=True, figsize=(5, 4))
ax[0].plot(sol.t, r_sol)
ax[1].plot(sol.t, theta_sol)
ax[0].set_ylabel("r [m]")
ax[1].set_ylabel("theta [rad]")
ax[1].set_xlabel("time [s]")
ax[0].grid()
ax[1].grid()
fig.tight_layout()
plt.show()
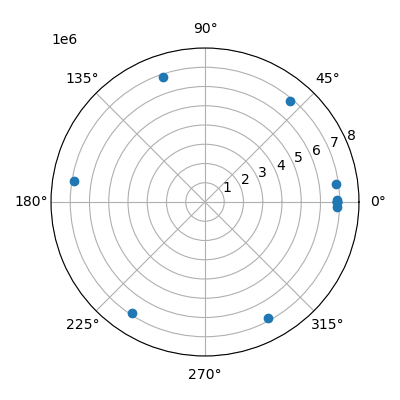
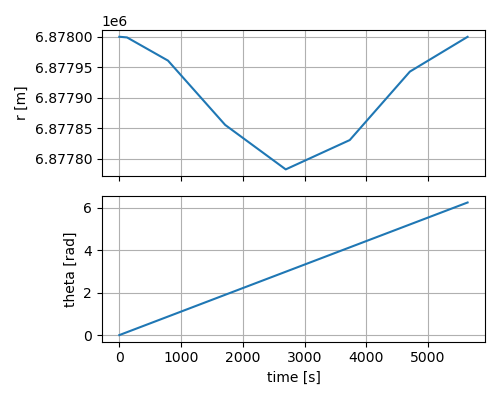
点が10個ほどしかなく疎らですが、初期と同じ高度6878 [km] (= 500+6378 [km])をほぼ維持した状態で、一定の角速度で地球を一周したことが分かります(途中で高度が200 [m]程度下がっているが、シミュレーション誤差によるもの)。
モルニア軌道 #
モルニア軌道は、軌道長半径26600 [m], 離心率0.74, 周期43200 [秒](12 [時間])の楕円軌道です。 \(r\)軸方向の初期位置は近点(地球と衛星が最も近くなる点)とします。近点と地球の中心(楕円の焦点)の距離\(r_p\)は次式で計算できます。
$$r_p = a_{sm} (1-e_{cc})$$ここで、\(a_{sm}\)は軌道長半径、\(e_{cc}\)は離心率です。
また、近点における速度\(v_p\)は次式となります。
$$v_p = \sqrt{GM\left( \frac{2}{r_p} - \frac{1}{a_{sm}} \right)}$$
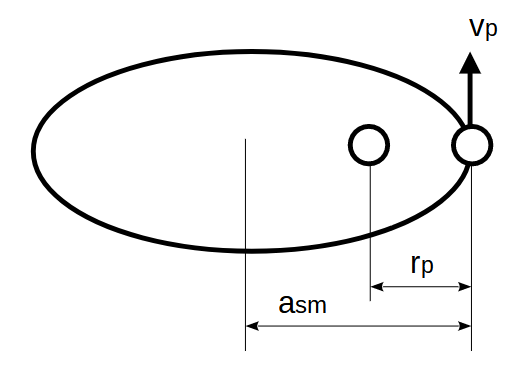
\(r\), \(\theta\)軸方向の初期位置をそれぞれ\(r_p\), 0 [rad] とします。また、初期角速度は\(v_p/r_p\)となります。
# モルニヤ軌道
asm = 26600e3 # 軌道長半径 [m]
ecc = 0.74 # 離心率 [-]
rp = asm*(1-ecc) # 近点距離(地球中心と近点の距離) [m]
vp = math.sqrt(GMe*(2/rp - 1/asm)) # 近点の速度 [m/s]
omega0 = vp/rp
x_init = [rp, 0, 0, omega0]
sol = solve_ivp(orbit, [0, 43200], x_init)
シミュレーション結果をプロットします。
r_sol = sol.y[0]
theta_sol = sol.y[1]
fig = plt.figure(figsize=(4, 4))
ax = fig.add_subplot(111, projection="polar")
ax.plot(theta_sol, r_sol, "o")
ax.plot(np.linspace(0, 2*np.pi, num=50), [Re]*50)
plt.show()
fig, ax = plt.subplots(nrows=2, sharex=True, figsize=(5, 4))
ax[0].plot(sol.t, r_sol)
ax[1].plot(sol.t, theta_sol)
ax[0].set_ylabel("r [m]")
ax[1].set_ylabel("theta [rad]")
ax[1].set_xlabel("time [s]")
ax[0].grid()
ax[1].grid()
fig.tight_layout()
plt.show()
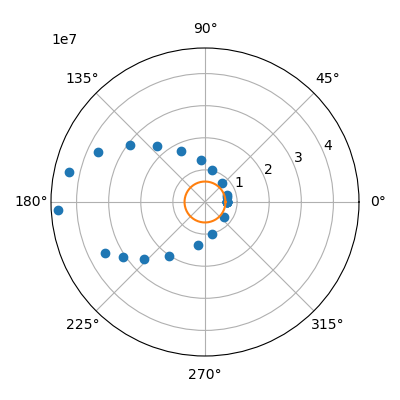
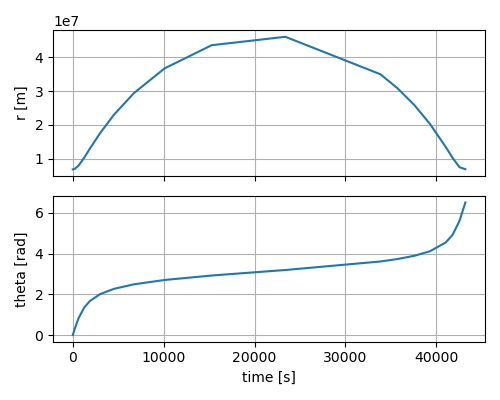
最初の図のオレンジ色の円は地球です。衛星は43200 [秒](12 [時間])で地球を1周していることが分かります。また、遠点高度は約40000 [km](=47000-6378 [km])であり、モルニア軌道のWikipediaの記述と一致しています。さらに、ケプラー法則の第2法則(面積速度一定の法則)の通り、遠点における角速度は近点の角速度より遅くなっています。
