はじめに #
説明変数が2つ以上ある回帰モデル(重回帰モデル)を作成するとき、相関が強い説明変数があると、推定結果が不安定になる。この問題は多重共線性、あるいは英語のmulti-collinearityからマルチコと呼ばれる。 本記事では、多重共線性が生じる原因について、数学的な厳密さを省いて直観的に説明する。
多重共線性が発生する原因 #
3つの変数\(x_1, x_2, x_3\)を用いて、変数\(y\)を予測する重回帰モデルを考える。 すなわち、回帰式は以下で表される。
$$ y=ax_1+bx_2+cx_3+d $$ただし、\(a, b, c\)は回帰係数、\(d\)は定数項である。
次に、データが下図のように与えられたとする。 図より、\(y\)は\(x_1\)と相関が高い一方で、\(y\)は\(x_2, x_3\)との相関は非常に低い。 すなわち、\(y\)の変化は\(x_1\)によってほぼ説明できる。 \(y\)の変化と\(x_1\)の変化は1:1であるので、回帰係数\(a\)は1である。
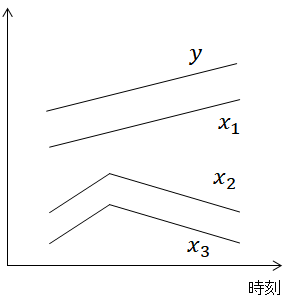
問題となるのは、相関の高い\(x_2, x_3\)の回帰係数\(b, c\)である。\(x_2\)の変化を\(x_3\)により打ち消せれば\(b, c\)の値は何でも良いので、\((b, c)=(1, -1)\)でも、極端な話、\((b, c)=(100, -100)\)でも良い。
すなわち、以下の回帰式が得られることもあり得る(簡単のため、定数項は無視した)。
$$ y= x_1+ 100 x_2 - 100 x_3 $$このような係数が大きい回帰式を用いてしまうと、\(x_2\)または\(x_3\)にノイズが入った場合、\(y\)の推定値が非常に大きく変化してしまう。 以上が、多重共線性により重回帰モデルの推定結果が不安定になる原因である。
多重共線性への対策 #
多重共線性への対策として正則化 (regularization) が挙げられる。正則化とは係数の大きさに対して罰則を加え、係数の絶対値をなるべく小さくする方法である。 すなわち、上記の例では係数\(b, c\)をともに0に近づけて、推定結果を安定させることができる。
正則化の方法にはいくつか種類があり、リッジ (Ridge) 回帰、ラッソ (Lasso) 回帰、Elastic Netと呼ばれるモデルが良く用いられる。 これらのモデルはscikit-learnに実装されており、以下の記事で使い方を解説している。
