はじめに #
次元削減 (dimensionality reduction) とは、データの構造をなるべく保ったまま、特徴量の数を減らすことである。 特徴量の数を減らすことにより、機械学習を高速に実行できたり、データの可視化をしやすくなる利点がある。
次元削減には、射影と多様体学習という2つの主なアプローチがある。射影を使った手法としては、主成分分析 (PCA, Principal Components Analysis) が有名である。一方、本記事で扱うLLEは、多様体学習と呼ばれるアプローチに属する。
多様体 #
多様体 (manifold) とは、簡単に表すと、局所的に低次元の超平面と見なせる図形のことである。 例えば、以下に示すSwiss Rollは、3次元空間のデータであるが、局所的には2次元の平面と見なせる。 すなわち、データから2次元平面をうまく見つけることができれば、構造を保ったまま3次元から2次元に圧縮できる。

このように、多様体のモデルを見つけることを多様体学習と呼ぶ。多様体学習には以下のように様々な手法がある。
- LLE
- 多次元尺度法 (multi-dimensional scaling, MDS)
- Isomap
- t-SNE (t-distributed Stochastic Neighbor Embedding)
- UMAP (Uniform Manifold Approximation and Projection)
LLEには大域的な位置関係を保存できる長所がある一方、以下の短所もある。
- 多様体が複数ある場合、互いの位置関係をうまく保存できない。
- 圧縮後のデータ位置を再構成する計算量がデータ数の2乗に比例するため、大規模なデータに適用しづらい。
LLEアルゴリズム #
LLEのアルゴリズムは、2つのステップでデータ間の局所的な線形モデルを構築し、次元を削減する。
- 局所的な関係の線形モデル化
- 関係を維持した次元削減
局所的な関係の線形モデル化 #
まず、データの各インスタンスに対して、近傍にあるk点のインスタンスを探し、それらインスタンスの線形結合で表すことを考える。ただし、kはハイパーパラメータである。
例として、下図のように2次元空間において5つの点A~Eが与えられた場合に、点Cを近傍インスタンスの線形和として表すことを考える。 k=2とすると、点Cの近傍インスタンスは点B, Dである。 また、点B, C, Dの位置は\(\boldsymbol{x^{(B)}, x^{(C)}, x^{(D)}}\)で与えられるとする。
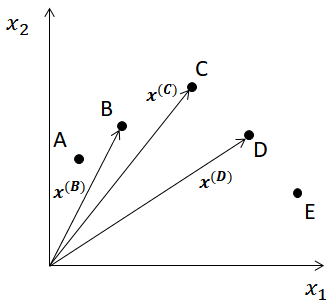
次に、\(\boldsymbol{x^{(B)}, x^{(D)}}\)の線形結合として次式を考える。
$$ w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}} $$ただし、\(w_{C, B}, w_{C, D}\)は点Cに対する点B, Dの重み係数である。 また、
$$ w_{C, B}+w_{C, D}=1 $$である。
さらに、点Cを点B, Dの線形結合で近似するため、次式が最小となる\(w_{C, B}, w_{C, D}\)を求める。
$$ \boldsymbol{x^{(C)}} - (w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}}) \\ \mathrm{subject\ to\ } w_{C, B}+w_{C, D}=1 $$下図は、上記の考えを幾何的に示したものである。 図の点B, Dを結ぶ破線は、\(\boldsymbol{x^{(B)}, x^{(D)}}\)の線形結合を表す。 また、求める係数\(w_{C, B}, w_{C, D}\)は、 \(w_{C, B}\boldsymbol{x^{(B)}} + w_{C, D}\boldsymbol{x^{(D)}}\) と \(\boldsymbol{x^{(C)}}\) の距離を最小とする値となる。

以上、ある点に対する線形モデル化を示したが、全ての点に対して一般化した式を示す。 インスタンスの数を\(N\)として、重み係数を行列\(W\in\mathbb{R}^{N\times N}\)にまとめる。 重み係数\(w_{i,j}\)を\(W\)の\((i,j)\)成分とする。 このとき、線形モデル化とは、次式を最小化する重み行列\(W\)を求める問題となる。
$$ \sum_{i=1}^{N} \left( \boldsymbol{x^{(i)}} - \sum_{j=1}^{N} w_{i,j} \boldsymbol{x^{(j)}} \right)^2$$$$ \mathrm{subject\ to\ } \begin{cases} \sum_{j=1}^{N} w_{i,j} = 1 & (\mathrm{for\ } i=1,2,...,N) \\\ w_{i,j} = 0 & (\boldsymbol{x^{(j)}} が \boldsymbol{x^{(i)}} の近傍点ではない) \end{cases} $$関係を維持した次元削減 #
前節で得られた重み行列\(W\)を用いて、データの局所的な関係をなるべく維持できるように、圧縮後の次元におけるインスタンスの位置を求める。 圧縮後のインスタンスの位置を\(\boldsymbol{y^{(i)} (i=1,2,...,N)}\)とする。 ただし、\(\boldsymbol{y^{(i)}}\)の次元は\(\boldsymbol{x^{(i)}}\)の次元より小さくなければならない。 このとき、\(\boldsymbol{y^{(i)}}\)は次式を最小化する値として得られる。
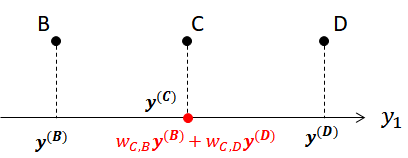
$$ \sum_{i=1}^{N} \left( \boldsymbol{y^{(i)}} - \sum_{j=1}^{N} w_{i,j} \boldsymbol{y^{(j)}} \right)^2 $$先程の例の続きで説明する。 2次元空間上の点B, C, Dの位置\(\boldsymbol{x^{(B)}, x^{(C)}, x^{(D)}}\)を1次元空間に圧縮するものとして、圧縮後の位置を\(\boldsymbol{y^{(B)}, y^{(C)}, y^{(D)}}\)とする。 得られた重み係数\(w_{C, B}, w_{C, D}\)を用いると、\(\boldsymbol{y^{(B)}}\)の最適な位置は次式で与えられる(下図参照)。
$$ w_{C, B}\boldsymbol{y^{(B)}} + w_{C, D}\boldsymbol{y^{(D)}} $$