はじめに #
Forward-backward envelope (FBE) に関する論文を読んだので、備忘録として残す。 FBEは滑らかではない凸最適化問題に対して、ニュートン法などを適用するための関数である。
滑らかでない(=微分不可能な)凸関数の最小化問題を解く手法として、forward-backward splitting (FBS) や近接勾配法 (proximal gradient method) などがある。 これらの手法は1次の勾配情報を使用するため、大規模な問題では収束が遅くなる。
P. PatrinosやL. Stellaらによって提案されたFBEは、元の最小化問題から得られる微分可能な関数である。 FBEを用いることでニュートン法等を適用でき、q-超1次収束 (superlinear convergence) ないしq-2次収束 (quadratic convergence) に収束性が向上する。
この記事では、まず対象となる問題およびその例としてLasso最適化を示す。 次に、FBEの導入として近接写像 (proximal mapping) とモーロー包 (Moreau envelope) について述べる。 最後に、FBEの定義と特徴をまとめている。
対象となる最小化問題 #
以下の最小化問題を考える。
$$ \mathrm{minimize} \ F(x) = f(x) + g(x) $$ここで、\(x \in \mathbb{R}^n\)であり、\(f(x)\)は微分可能な凸関数、\(g(x)\)は微分可能とは限らない凸関数とする。
このような最小化問題の例としてLasso回帰が挙げられる。 Lasso回帰の最小化問題は、
$$ \min_{\bm{w}} \left\{ \sum_{i=1}^{N} (y_i - \bm{w}^\top \bm{x}_i)^2 + C || \bm{w} ||_1 \right\} $$と記述される。ここで、\(N\)はデータ点数、\(\bm{w}\)は係数ベクトル、\(C\)は正則化の強さに関する重み係数、\(|| \cdot ||_1\)はL1ノルムである。 この場合、\(f(x), g(x)\)は以下のようになる。
$$ f(x) = \sum_{i=1}^{N} (y_i - \bm{w}^\top \bm{x}_i)^2 $$$$ g(x) = C || \bm{w} ||_1 $$
近接写像とモーロー包 #
まず、近接写像とモーロー包について述べる。 滑らかとは限らない凸関数\(g(x)\)に対する近接写像は次式で定義される。
$$ \mathrm{prox}_{\gamma g} (x) := \argmin_u \left\{ g(u) + \frac{1}{2 \gamma} || u - x ||^2 \right\} $$大雑把にいえば、近接写像とは\(x\)の近傍において、関数\(g\)を最小化する\(u\)を求めるものである。 ユークリッド距離の2乗の項\(|| u - x ||^2\)によって、\(u\)がなるべく\(x\)の近傍に留まるようにしている。 なお、\(\gamma\)は、近接写像を用いた最適化手法である近接勾配法における、解の更新幅に対応する。
また、次式で定義される\(g^\gamma (x)\)を、\(g(x)\)のモーロー包と呼ぶ。
$$ g^\gamma (x) := \min_u \left\{ g(u) + \frac{1}{2 \gamma} || u - x ||^2 \right\} $$モーロー包は滑らかな凸関数である。
FBEの定義と特徴 #
最初に示した最小化問題の関数\(F(x)=f(x)+g(x)\)に対し、FBEは次式の\(F_\gamma (x)\)で定義される。
$$ F_\gamma (x) := f(x) - \frac{\gamma}{2} || \nabla f(x) ||_2^2 + g^\gamma (x - \gamma \nabla f(x)) $$また、FBEは以下のようにも記述できる。
$$ \begin{array}{ll} F_\gamma (x) &= \min_{u \in \mathbb{R}^n} \left\{ f(x) + \nabla f(x)^\top (u-x) + g(u) + \frac{1}{2\gamma} ||u-x||^2 \right\} \\\ &= f(x) +g(P_\gamma (x)) - \gamma \nabla f(x)^\top G_\gamma (x) + \frac{\gamma}{2} ||G_\gamma (x)||^2 \end{array} $$ただし、
$$ P_\gamma (x) := \mathrm{prox}_{\gamma g} (x - \gamma \nabla f(x)) $$$$ G_\gamma (x) := \gamma^{-1} (x - P_\gamma (x)) $$
である。
FBEである\(F_\gamma\)について以下の性質が成り立つ。
- \(F_\gamma\)は連続微分可能であり、勾配は次式となる。
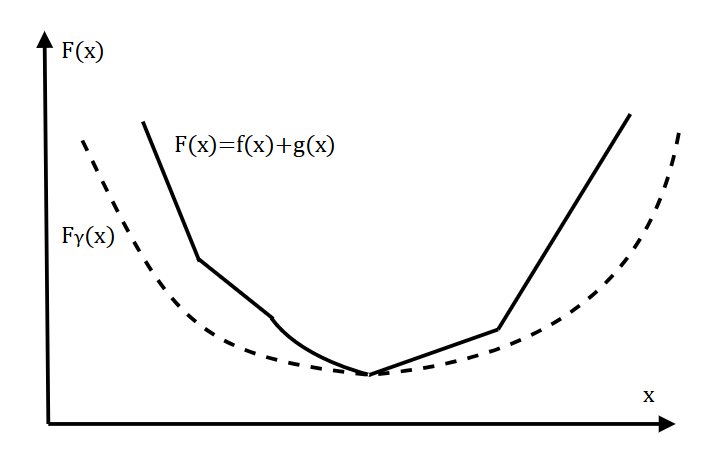
- \(\gamma \in (0, 1/L_f)\)のとき、\(F\)の最適解と\(F_\gamma\)の最適解は一致し、そのときの目的関数の値も一致する。すなわち、以下が成り立つ(画像参照)。
参考 #
FBEの論文。
- Forward-backward truncated Newton methods for convex composite optimization (arXiv)
- Forward-backward quasi-Newton methods for nonsmooth optimization problems (arXiv)
近接写像に関して、以下の記事・書籍を参考にさせていただいた。
