はじめに #
CVaR (Conditional Value at Risk) によるリスクを評価したポートフォリオ最適化手法について、“Optimization Methods in Finance"を読んで勉強した内容をまとめました。
金融工学の分野では、株価などが変動する確率を計算して、リスクを最小化(または利益を最大化)する株式や債券の組み合わせ(ポートフォリオ)を構築します。CVaRは確率的な事象のリスクを考慮するための尺度で、例えば損失が一定の範囲に収まるポートフォリオの決定に用いられます。
この記事の内容は以下の通りです。
- VaR (Value at Risk)
- CVaR
- VaRとCVaRの比較
- CVaRを用いたシナリオ法によるポートフォリオ最適化
VaRはCVaRの基礎となるリスク評価指標です。また、シナリオ法とは、株価などの過去のデータや、シミュレーションにより生成したデータを最適化に用いる手法です。
VaR #
ある期間における投資の損失が、確率分布で表せるとします。VaRは、ある確率\(\alpha\)(95%など)における最大の損失を意味します。すなわち、\(\alpha=0.95\)とした場合、100回投資をした中の95回では、損失はVaRの値より小さくなることを意味します。“Optimization Methods in Finance"では、\(\alpha\)のことをprobability levelと呼んでいますが、日本語の資料では信頼水準や信頼区間と呼ぶことが多いようです。
\(X\)を投資の損失、\(\gamma\)を信頼水準の範囲内における最大の損失とすると、信頼水準\(\alpha\)におけるVaRは次式で定義されます。
$$VaR_{\alpha}(X) := \min \\{\gamma : P(X \ge \gamma) \le 1 - \alpha \\}$$以下のグラフは確率密度関数とVaRの関係を示しています。\(\alpha=0.95\)であり、青で塗りつぶされた面積が\(1-\alpha=0.05\)となります。
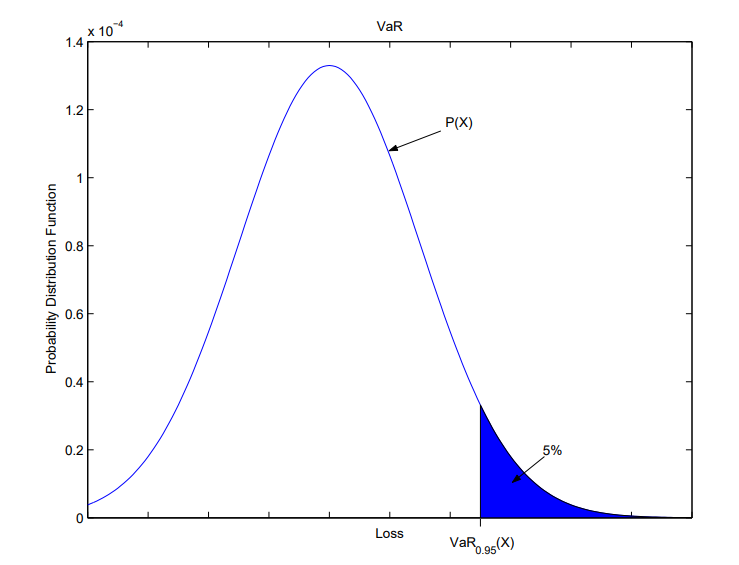
VaRは金融工学で幅広く使われています。しかし、VaRを使ったポートフォリオ最適化を計算しようとしても、最適化問題が非平滑や非凸となるため、計算が困難となる課題があります。
さらに、VaRには、信頼水準を超える領域の損失を扱っていないという短所があります。例えば、100回中1回巨大な損失を出す投資対象があったとしても、\(\alpha=0.95\)などとしたVaRには表現されません。 そのため、損失の期待値を計算するCVaRが考案されています。
CVaR #
ポートフォリオの決定(投資の割合)に関するベクトルを\(x\), ランダムなイベントのベクトルを\(y\)とします(両者の次元は異なっていても構いません)。損失は\(x\)と\(y\)によって決まるため、損失を関数\(f(x, y)\)として表します。また、\(y\)は確率密度関数\(p(y)\)によって得られるとします。
次に、\(x\)を固定した状態における、損失の確率密度関数を積分した関数、すなわち累積分布関数 (cumulative distribution function) を考えます。累積分布関数は次式で定義されます。
$$\Psi (x, \gamma) := \int_{f(x, y) < \gamma} p(y) dy$$累積分布関数\(\Psi (x, \gamma)\)に対し、信頼水準\(\alpha\)のVaRを次式で定義します。
$$VaR_{\alpha}(x) := \min \\{\gamma : \Psi(X, \gamma) \ge \alpha \\}$$これを用いて、信頼水準\(\alpha\)のCVaRを次式で定義します。
$$CVaR_{\alpha}(x) := \frac{1}{1-\alpha} \int_{f(x, y) \ge VaR_{\alpha}(x)} f(x, y)p(y) dy$$右辺の積分を日本語にすると、「VaRを超える損失\(f(x,y)\)に対して、その発生確率\(p(y)\)を掛けて積分する」になります。
すなわち、CVaRとは、水準を超える損失に確率を掛けて積分した値になります。また、確率\(1-\alpha\)で割ることにより、VaRと同じ次元にしていると個人的に解釈しています。証明は省略しますが、信頼水準\(\alpha\)が同じ場合、CVaRの値はVaRの値以上となります。
$$CVaR_{\alpha}(x) \ge VaR_{\alpha}(x)$$また、確率分布が離散値を取る場合、信頼水準\(\alpha\)のCVaRは次式で計算されます。
$$CVaR_{\alpha}(x) := \frac{1}{1-\alpha} \sum_{j: f(x, y) \ge VaR_{\alpha}(x)} f(x, y_j) p_j$$ここで、イベント\(y_j\)が確率\(p_j\)で発生するとします。
VaRとCVaRの比較 #
数値例を通してVaRとCVaRを比較します。
ある会社の株に対して1万円を1日だけ投資することを100回繰り返したとします(単元株などの細かい話は無視します)。このとき、投資の損失のデータが100個得られることになります。この損失を大きい順に並び変えると、以下の表になったとします(マイナスの損失は利益が出たことを意味します)。
| 日 | 損失(円) |
|---|---|
| 3 | 950 |
| 76 | 920 |
| 44 | 910 |
| 92 | 820 |
| 24 | 800 |
| 29 | 790 |
| … | … |
| 13 | -930 |
| 56 | -960 |
各行の損失の発生確率は、それぞれ1%となります。よって、信頼水準を\(\alpha=0.95\)とすると、VaRの値は上から5行目、すなわち以下になります。
$$VaR_{0.95}(X) = \min \\{\gamma : P(X \ge \gamma) \le 0.05 \\} = 800$$これは「5%の確率で損失は800円以上になる」ことを意味します。
一方、CVaRの値は1~5行目の損失の値を用いて、以下の通り計算されます。
$$ CVaR_{0.95}(X) = \frac{1}{1-0.95} \sum_{j: f(x, y_j) \ge VaR_{0.95}(x)} f(x, y_j) p_j \\\ = \frac{1}{1-0.95} (950+920+910+820+800) \times 0.01 = 880 $$これは「ワースト5%の確率で発生する損失を確率で重み付け平均すると880円になる」ことを意味します。 また、以下の関係も確認できました。
$$CVaR_{0.95}(x) = 880 \ge 800 = VaR_{0.95}(x)$$CVaRを用いたシナリオ法によるポートフォリオ最適化 #
CVaRを用いたポートフォリオ最適化問題を考えます。ここでは、CVaRを評価関数として最小化します。この問題は、\(1-\alpha\)の確率で発生する損失を最小化する問題であると言い換えることができます。なお、評価関数を期待リターンとCVaRの重み付け和とするなどの工夫も可能です。
前節のCVaRの定義式にはVaRが含まれており最適化に向かないため、以下の補助関数を定義します。
$$F_{\alpha} (x, \gamma) := \gamma + \frac{1}{1-\alpha} \int_{f(x, y) \ge \gamma} (f(x, y) - \gamma) p(y) dy \\\ = \gamma + \frac{1}{1-\alpha} \int (f(x, y) - \gamma)^{+} p(y) dy$$ここで、\(a^{+} = \max \{a, 0 \}\)を意味します。上記の補助関数は以下の性質を持ちます。
- \(F_{\alpha} (x, \gamma)\)は\(\gamma\)に対して凸である。
- \(F_{\alpha} (x, \gamma)\)を\(\gamma\)に対して最小化した値は\(CVaR_{\alpha}(x)\)に等しい。
すなわち、次式の通り\(CVaR_{\alpha}(x)\)を最小化する\(x\)を求めることは、\(F_{\alpha} (x, \gamma)\)を最小化する\(x, \gamma\)を求める問題に等しくなります。
$$\min_{x \in X} CVaR_{\alpha}(x) = \min_{x \in X, \gamma} F_{\alpha} (x, \gamma)$$\(F_{\alpha} (x, \gamma)\)を最小化するにあたって、確率密度関数\(p(x)\)の計算または決定が困難な場合が多いです。そこで、シナリオ法を使った\(F_{\alpha} (x, \gamma)\)の最小化が提案されています。シナリオ法とは、(株価などの)過去のデータや、シミュレーションにより生成したデータを最適化に用いる手法です
シナリオの数を\(S\)とし、各シナリオを\(y_s (s = 1, ..., S)\)と表します。各シナリオの発生確率は等しいとします。\(F_{\alpha} (x, \gamma)\)の近似式を次式で定義します。
$$ \tilde{F_{\alpha}} (x, \gamma) := \gamma + \frac{1}{(1-\alpha)S} \sum_{s=1}^{S} (f(x, y_s) - \gamma)^{+} $$この近似式を用いて、CVaR最小化問題は次の最小化問題に近似されます。
$$\min_{x \in X, \gamma} \gamma + \frac{1}{(1-\alpha)S} \sum_{s=1}^{S} (f(x, y_s) - \gamma)^{+}$$さらに、\((f(x, y) - \gamma)^{+}\)が最適化で扱いづらいため、変数\(z_s\)を導入して置き換えます。
$$\min_{x, z, \gamma} \gamma + \frac{1}{(1-\alpha)S} \sum_{s=1}^{S} z_s \\\ \mathrm{s.t.} z_s \ge f(x, y_s) - \gamma \ (\forall s), \\\ z_s \ge 0 \ (\forall s)$$もし\(f(x, y)\)が線形であれば、この最適化問題は線形となります。すなわち、線形ソルバを使用して解くことが可能となります。
例題 #
N個の会社に対する投資の割合を決める問題を考えます。投資の配分を\(x_i (i=1, ..., N)\)とします(合計は1とします)。
各社の過去S日分の損失が得られているものとして、i社のs日目の損失を\(l_{i, s}\)とします。このとき、シナリオ法によるCVaR最小化問題は以下のように定式化されます。
$$\min_{x, z, \gamma} \gamma + \frac{1}{(1-\alpha)S} \sum_{s=1}^{S} z_s \\\ \mathrm{s.t.} z_s \ge \sum_{i=1}^{N} l_{i,s} x_i - \gamma \ (\forall s), \\\ z_s \ge 0 \ (\forall s), \\\ \sum_{i=1}^{N} x_i = 1 \\\ 0 \le x_i \le 1 \ (\forall i) $$これは線形最適化問題となります。なお、\(\alpha\)の値は事前に決定する必要があります。
参考文献 #
この記事は数理最適化 Advent Calendar 2022の4日目の記事です。
